МИНИМАЛЬНОЕ МНОЖЕСТВО

-1) M. м. в римановом пространстве - обобщение минимальной поверхности. М . м. есть k-мерное замкнутое подмножество Х ₀ в римановом пространстве М ^п, n>k, такое, что за исключением подмножества Z k -мерной хаусдорфовой мера нуль множество является дифференцируемой й-мерной минимальной поверхностью (т. е. экстремалью функционала k-мерного объема , определенного на k-мерных поверхностях, вложенных в М ⁿ). Понятие "М. м." объединяет в себе несколько математич. понятий, призванных обслуживать так наз. многомерную Плато задачу.

А. Т. Фоменко.

2)М. м. топологической динамической системы 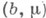- такое непустое замкнутое инвариантное (т. е. целиком состоящее из траекторий) подмножество Fфазового пространства Wсистемы, к-рое не имеет собственных замкнутых инвариантных подмножеств. Последнее эквивалентно тому, что каждая из лежащих в Fтраекторий всюду плотна в F. Понятие М. м. ввел Дж. Биркгоф (G. Birkhoff, см. [1]) применительно к случаю потока ("время" tпробегает действительные числа). Он доказал (см. [1], [2]), что если F- компактное М. м. ис 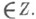, то для любой окрестности Uточки wмножество тех t, для к-рых 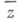относительно плотно (т. е. имеется такое l, что в каждом "отрезке времени" [s, s+l]длины lсодержится хоть одно ( с ); обратно, если W- полное метрич. пространство и точка wобладает указанным выше свойством, то замыкание траектории {S_tw}- компактное М. м. (то же самое справедливо и для каскадов;оболее общих группах преобразований см., напр., [3] или [4]). Сформулированное свойство точки 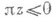(и ее траектории) Дж. Биркгоф назвал рекуррентностью этой точки (и траектории), употребителен также предложенный У. Готшалком и Г. Хедлундом [3] другой вариант терминологии, в к-ром это свойство наз. почт и-периодичностью точки w. Если 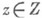, то саму динамич. систему называют минимальной.

Если нек-рая траектория имеет компактное замыкание, то в нем содержится нек-рое М. м. F(для полугрупп непрерывных преобразований {S_t} с неотрицательными действительными или целыми tсправедлив аналог этого результата, причем на Fпреобразования S_t уже обратимы [5]). Однако исследование предельного поведения траекторий динамич. системы не сводится к изучению одних только М. м. последней. Очень просто устроено М. м. гладкого потока класса С ² на двумерной замкнутой поверхности - это либо точка, либо замкнутая траектория, либо вся поверхность, к-рая в этом случае является тором (теорема Шварца, см. [6]). В общем случае строение М. м. может быть весьма сложным (в связи с этим, дополнительно к сказанному в [2] - [4], надо указать, что минимальность динамич. системы не накладывает никаких ограничений на ее эргодич. свойства по отношению к имеющимся у нее инвариантным мерам [7]). М. м. - основной объект изучения в топологической динамике.

Лит..:[i] Биркгоф Дж . Д., Динамические системы, пер. с англ., М.-Л., 1941; [2] Немыцкий В. В., Степанов В. В., Качественная теория дифференциальных уравнений, 2 изд., М.-Л., 1949; [3] Gоttsсhalk W. H., Hedlund G. A., Topological dynamics, Providence, 1955; [4]Бронштейн И. У., Расширения минимальных групп преобразований, Киш., 1975; [5] Левитан Б. М., Жиков В. В., Почти-периодические функции и дифференциальные уравнения, М., 1978; [6] Хартман Ф., Обыкновенные дифференциальные уравнения, пер. с англ., М., 1970; [7] Итоги науки и техники. Математический анализ, т. 13, М., 1975, с. 129-262. Д. <В. Аносов.