МЕТРИЧЕСКИЙ ИЗОМОРФИЗМ

пространств с мерой 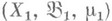и - биективное отображение при к-ром образы и прообразы измеримых множеств измеримы и имеют ту же меру (здесь - нек-рая булева -алгебра или -кольцо подмножеств пространства 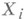, называемых измеримыми, а - заданная на мера). Волее общее понятие - (метрический) гомоморфизм этих пространств, т. е. такое отображение 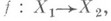что прообразы измеримых множеств измеримы и имеют ту же меру. При вместо изоморфизма или гомоморфизма говорят о (метрическом) автоморфизме или эндоморфизме.

В соответствии с обычной в теории меры тенденцией пренебрегать множествами меры нуль вводятся (и преимущественно используются) варианты всех этих понятий "по mod 0". Напр., пусть 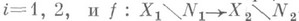- М. и.; тогда говорят, что f есть изоморфизм исходных пространств с мерой по mod 0. (Оговорку "по mod 0" часто опускают.)

Для ряда объектов, заданных в 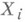(подмножеств, функций, преобразований, а также их систем), имеет смысл утверждение, что при М. и. f эти объекты переходят друг в друга. Тогда говорят, что f есть М. и. соответствующих объектов. Можно говорить также об их М. и. по mod 0. При этом подразумевается, что при нек-рых меры нуль соответствующие объекты могут рассматриваться как нек-рые объекты 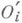в 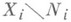(для преобразований это означает, что 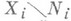инвариантны относительно этих преобразований, а для подмножеств и функций это имеет смысл при любых - надо взять пересечения рассматриваемых подмножеств с и ограничения функций на) 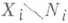и что f есть М. и. объектов 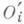. Класс всех метрически изоморфных по mod 0 друг другу объектов называют (метрическим) типом; говорят, что два объекта из этого класса имеют одинаковый тип.

С ассоциируются гильбертово пространство 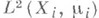, в к-ром дополнительно к обычной структуре гильбертова пространства имеется еще операция обычного перемножения функций (определенная, правда, не всюду, ибо произведение функций из не всегда принадлежит ), и булева s-алгебра с мерой , получающаяся из отождествлением множеств, симметрич. разность к-рых имеет меру нуль (т. е. факторизацией по идеалу, состоящему из множеств меры нуль). М. и. mod 0 f индуцирует, изоморфизм булевых -алгебр с мерой 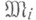и унитарный изоморфизм гильбертовых пространств , к-рый мультипликативен, т. е. переводит произведение (когда оно определено) в произведение образов сомножителей. Если - Лебега пространство, то верно и обратное: всякий изоморфизм булевых 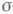-алгебр с мерой или мультипликативный унитарный изоморфизм пространствиндуцируется нек-рым М. и. по mod 0.

Лит.:[1] Рохлин В. А., "Матем. сб.", 1949. т. 25, № 1, с. 107 - 50.

Д. В. Аносов,