ЭНТРОПИЯ

метрическая динамической системы - один из важнейших инвариантов в эргодической теории. Основным является понятие Э. h(S)эндоморфизма S (см. Метрический изоморфизм) Лебега пространства Для любого конечного измеримого разбиения существует предел (энтропия на единицу времени относительно S)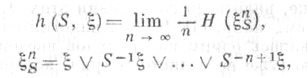

где 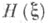-энтропия измеримого разбиения а 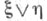- разбиение, элементы к-рого суть пересечения элементов разбиений и 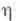(это определение дословно переносится на с 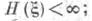другим способом определяется для любых измеримых Э. h(S)определяют как верхнюю грань по всевозможным конечным измеримым (они может равняться использование всех с 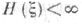или всех измеримых 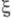дает ту же Э.).
Первоначально Э. была определена А. Н. Колмогоровым несколько иначе (см. [1]); приведенный выше вариант был дан позже (см. [2]). В основном случае апериодического автоморфизма пространства Лебега определения в конечном счете - эквивалентны [3].
Оказывается, что h(Sⁿ)=nh(S). аесли S - автоморфизм, то h(S^-1)=h(S). Поэтому Э. каскада{Sⁿ}естественно считать h(S). Для измеримого потока{S_t} оказывается, что h(S_t)=|t|h(S₁). Поэтому Э. потока естественно считать h(S₁). Несколько иначе определяется Э. для других групп преобразований с инвариантной мерой (она уже не сводится к Э. одного из преобразований, входящих в эту группу; см. [5], [6]). Имеется модификация Э. для случая бесконечной инвариантной меры [7]; еще одна модификация - А - энтропия (где А = {k,,} - возрастающая последовательность натуральных чисел) - получается при замене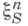 на 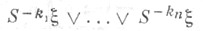и lim на (см. [8]).
Э. является инвариантом метрического изоморфизма динамич. систем, принципиально отличным от известных ранее инвариантов, в основном связанных со спектром динамической системы. В частности, с помощью энтропии Бернулли автоморфизмов (см. [1]) впервые установлено существование неизоморфных яргодич. систем с одинаковым непрерывным спектром (что контрастирует с ситуацией для дискретного спектра). В более широком плане роль Э. связана с тем, что вместе с ней п эргодич. теории возникло новое направление - энтропийная теория динамич, систем (см. [3], [4] и эргодическая теория).
Э. дает нек-рую среднюю характеристику скорости перемешивания множества малой меры (точнее, набора таковых, образующих разбиение). Наряду с этой лглобальной