ЭНТРОПИЙНАЯ ТЕОРИЯ ДИНАМИЧЕСКИХ СИСТЕМ

- раздел эргодической теории, тесно связанный с теорией вероятностен и теорией информации. Природа этой связи в общих чертах такова.
Пусть {T_t} - динамич. система (обычно измеримый поток или каскад )с фазовым пространством Wи инвариантной мерой Пусть - измеримая функция, а - измеримое разбиение W на прообразы (для дальнейшего достаточно рассматривать прообразы f, имеющей счетное, обычно даже конечное, число значений и соответствующие Тогда 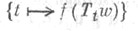есть стационарный (в узком смысле слова) случайный процесс с пространством элементарных событий W. 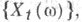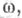Обычным образом этот процесс можно рассматривать как процесс пространством элементарных событий к-рого служит пространство выборочных функций снабженное надлежащей мерой v, a Отображение

является гомоморфизмом пространств с мерой (см. определение в ст. Метрический изоморфизм), переводящим { Т _t} всдвиги {S_t},где
Процесс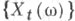 содержит нек-руго информацию об исходной системе { Т _t}. Это может быть даже полная информация, если я - изоморфизм (тогда говорят, что разбиение - образующее для системы { Т _t}; если Т- автоморфизм, то разбиение наз. односторонне образующим для Т, если оно является образующим для каскада и двусторовне образующим для Т, если оно - образующее для Однако 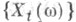зависит также от выбора f, т. е. прежде всего от (конкретные значения f на элементах здесь менее важны). Для эргодической теории интересны те свойства индивидуального процесса или совокупности таких процессов (получающихся при различных к-рые являются свойствами самой системы { Т _t}. Однако выделить такие свойства долго не удавалось либо они сводились к известным.
Эту трудность удалось преодолеть в середине 50-х гг. 20 в. А. II. Колмогорову, к-рый ввел принципиально новый (неспектральный) инвариант - метрич. энтропию динамич. системы - и подчеркнул роль возрaстающих измеримых разбиений (уже континуальных), т. е. таких, для к-рых мельче (mod 0) при t>0. (Таким является разбиение, описывающее лпрошлое