- МАРКОВСКИЙ МОМЕНТ
- понятие, используемое в теории вероятностей для случайных величин, обладающих свойством независимости от "будущего". Точнее, пусть
- нек-рое измеримое пространство с выделенным на нем неубывающим семейством 
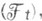
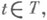s-подалгебр 
в случае непрерывного времени и Т={0, 1 ...} в случае дискретного времени). Случайная величина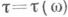 
со значениями в 
наз. марковским моментом (относительно семейства 
), если при каждом 
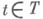событие 
принадлежит 
В случае дискретного времени это эквивалентно тому, что для любого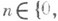 
событие 
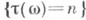принадлежит 
Примеры. 1) Пусть X(t),
- действительный случайный процесс, заданный на 
и 
Тогда случайные величины
в 
т. е. моменты (первого и первого после +0) достижения (борелевского) множества В, являются М. м. (в случае
полагают 
).
2) Если W(t),
- стандартный винеровский процесс то М. м.
имеет плотность распределения вероятностей
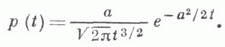
При этом
но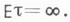 
3) Случайная величина
являющаяся первым моментом, после к-рого процесс Xt остается в множестве В, является примером немарковского момента (случайной величины, зависящей от "будущего").
С помощью понятия М. м. формулируется строго марковское свойство марковских процессов. М. м. и моменты остановки (т. е. конечные М. м.) играют важную роль в общей теории случайных процессов и статистическом последовательном анализе.
Лит.:[1] Г и х м а н И. И., Скороход А. В., Теория случайных процессов, т. 2, М., 1973. А. Н. Ширяев.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
