МАРКОВА ПРОБЛЕМА СПЕКТРА

проблема теории чисел, возникшая в связи с задачей о распределении нормированных значений арифметич. минимумов неопределенных бинарных квадратичных форм. Пусть

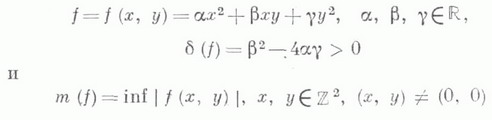- однородный арифметич. минимум формы f/.

Число

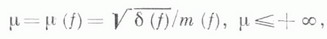
наз. постоянной Маркова формы f. Множество 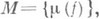когда f пробегает все действительные неопределенные квадратичные формы, наз. спектром Маркова. Постоянную и спектр Маркова определяют по-разному, в частности А. А. Марков в [1] рассматривал множество {2/m(f)}. Известно, что m(f) - инвариант луча Fклассов форм, т. е. множества

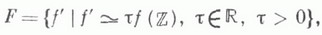
т. <к. m(f')=m(f)=m(F). Каждому лучу классов Fвзаимно однозначно сопоставляется двоякобесконеч-ная (бесконечная в обе стороны) последовательность

так, что если обозначить

(знак [; . . .] - обозначение цепной дроби), то

Проблему Маркова можно сформулировать следующим образом: 1) описать спектр Маркова М,2) для каждого описать множество форм f=f(x, у).(или лучей классов F), для к-рых m(f)=m(F).m. Проблема решена А. А. Марковым для начальной части спектра М, определяемой условием m(f)<3. Эта часть спектра является дискретным множеством

с единственной предельной точкой 3 (точка конденсации множества М); т, п, р пробегают все целые положительные решения диофантова уравнения Маркова

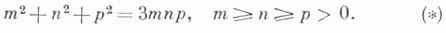
При этом каждой точке этой части спектра отвечает ровно один луч классов F_m, задаваемый формой Маркова f_m=f_m(x, у), с условием

Решение ( т, п, р).диофантова уравнения (*) наз. т р о й к о й Маркова; число т - ч и с л о м Маркова. Форма Маркова f_m следующим образом сопоставляется числу Маркова m=max(m, п, р):пусть r, определены условиями

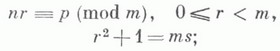
тогда, по определению,

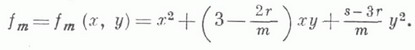
Множество М - замкнуто, и имеется такое число m₀=4,5278..., что и к m₀ примыкает интервал смежности множества М.

Проблема Маркова тесно связана с проблемой Лагранжа - Гурвица рациональных приближений к действительному числу 6. Величина

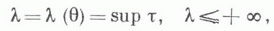
где точная верхняя граница берется по всем 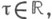t>0, для к-рых неравенство

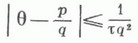
имеет бесконечное множество решений 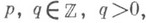наз. постоянной Лагранжа. Множество наз. спектром Лагранжа. Первым результатом в теории спектра Лагранжа естественно считать теорему Лагранжа: все

подходящие дроби разложения числа в в цепную дробь удовлетворяют неравенству

Если т. е. если

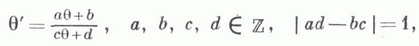
то где - класс эквивалентных чисел. Если q разложено в цепную дробь 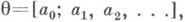то

Таким образом, проблему Лагранжа - Гурвица можно сформулировать так: 1) описать спектр Лагранжа L;2) для каждого 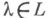описать множество чисел q (или классов ), для к-рых

Для l(q)<3 эта задача сводится к проблеме Маркова, причем

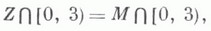
и каждому отвечает ровно один класс чисел q, описываемых формой Маркова f_m. Доказано, что L, как и М,- замкнутое множество, что 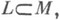но что

Причем к m₀ примыкает интервал смежности множества L. Исследования по структуре L и по связи Lи М описаны в [6]. Об обобщениях и аналогах проблемы спектра Маркова и о "явлении изоляции" см. [2], [3], [7].

Лит.:[1] М а р к о в А. А., "Успехи матем. наук", 1948, т. 3, в. 5, с. 7-51; [2] К а с с е л с Д ж. В. С., Введение в теорию диофантовых приближений, пер. с англ., М., 1961; [3] Делоне Б. Н., Петербургская школа теории чисел, М.- Л., 1947; [4] Горшков Д. С., "Зап. научи, семинаров Ленингр. отд. Матем. ин-та АН СССР", 1977, т. 67, с. 39-85; [5] Ф р е й м а н Г. А., Диофантовы приближения и геометрия чисел. (Задача Маркова), Калинин, 1975; [6] Малышев А. В., "Зап. научн. семинаров Ленингр. отд. Матем. ин-та АН СССР", 1977, т. 67, с. 5-38; [7] В е н к о в Б. А., "Изв. АН СССР. Сер. матем.", 1945, т. 9, с. 429-94. А. В. Малышев.