ЛИУВИЛЛЯ УРАВНЕНИЕ

ЛИУВИЛЛЯ УРАВНЕНИЕ

- уравнение движения для функции распределения wN(p, q; t).по импульсам и координатам N- частичной классич. системы

где H - гамильтониан системы, а фигурными скобками обозначены классич. скобки Пуассона.

Если в фазовом пространстве ( р, q).распределению wN(p, q; t).сопоставить плотность фазовых точек (каждая из к-рых соответствует определенному механич. состоянию данной системы Nматериальных точек), то в силу того, что траектории движения этих точек не пересекаются вследствие единственности решений уравнений движения механики, и того, что фазовый объем согласно Лиувилля теореме сохраняется, ансамбль этих точек образует в фазовом пространстве своеобразную несжимаемую жидкость, полная производная плотности к-рой wN по времени равна нулю:

Это приводит к Л. у., если только выразить согласно Гамильтона уравнениям производные от координат и импульсов через соответствующие частные производные от гамильтониана.

Л. у. используется не только при рассмотрении общих вопросов статистич. механики, связанных с выяснением микроскопической и макроскопической структур состояния системы многих тел, процессов стремления к равновесию, проблем "перемешивания" в фазовом пространстве, эргодичности и т. д., но и в конкретных исследованиях, т. к. Л. у. является исходным уравнением при построении Боголюбова цепочки уравнений, а следовательно, и для различного типа кинетич. уравнений, с помощью к-рых решаются уже прикладные физич. задачи.

В случае квантовых систем роль Л. у. играет уравнение движения для статистич. оператора 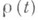(плотности матрица), к-рое в шрёдингеровском временном представлении имеет вид

где Н - оператор Гамильтона, а фигурными скобками обозначены квантовые скобки Пуассона. Это квантовое Л. у. является следствием структуры смешанного состояния (описываемой данным статистич. оператором), в к-ром каждое из составляющих его чистых квантово-механич. состояний эволюционирует согласно Шрёдингера уравнению.

Лит.:[1] Голдстейн Г., Классическая механика, пер. с англ., М., 1957; [2] У л е н б е к Д., Форд Д ж., Лекции по статистической механике, пер. с англ., М., 1965; [3] Боголюбов Н. Н., Избр. труды, т. 2, К., 1970.

И. А. Квасников.



Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.

Игры ⚽ Нужно сделать НИР?

Полезное


Смотреть что такое "ЛИУВИЛЛЯ УРАВНЕНИЕ" в других словарях:

  • ЛИУВИЛЛЯ УРАВНЕНИЕ — ур ние для ф ции распределения плотности вероятности частиц в фазовом пространстве основное ур ние статистич. физики. Ур ние для статистич. оператора ( матрицы плотности )в квантовой статистич. механике также наз. Л. у., но иногда уравнением фон… …   Физическая энциклопедия

  • ШТУРМА - ЛИУВИЛЛЯ УРАВНЕНИЕ — обыкновенное дифференциальное уравнение 2 го порядка вида рассматриваемое на конечном или бесконечном интервале ( а, b)изменения переменном х, где р(х), l (х), r (х) заданные коэффициенты, комплексный параметр, a у искомое решение. Если р(x),r… …   Математическая энциклопедия

  • ЛИУВИЛЛЯ ТЕОРЕМА — теорема механики, утверждающая, что фазовый объём системы, подчиняющейся ур ниям механики в форме Гамильтона (см. КАНОНИЧЕСКИЕ УРАВНЕНИЯ МЕХАНИКИ), остаётся постоянным при движении системы. Теорема установлена франц. учёным Ж. Лиувиллем (J.… …   Физическая энциклопедия

  • Уравнение Фоккера — Планка — Эволюция функции плотности вероятности согласно уравнению Фоккера  Планка. Уравнение Фоккера  Планка  одно из стохастических дифференциальных уравнений, описывает временную эволюцию функции плотности вероятности координат и… …   Википедия

  • Уравнение Лиувилля — В математической физике, теорема Лиувилля, названная по имени французского математика Жозефа Лиувилля, является ключевой теоремой в статистической и гамильтоновой механике. Она гласит, что функция распределения в фазовом пространстве постоянна… …   Википедия

  • Уравнение движения — (уравнения движения)  уравнение или система уравнений, задающие закон эволюции механической или сходной динамической системы (например, поля) во времени[1]. Эволюция физической системы однозначно определяется уравнениями движения и… …   Википедия

  • Уравнение фон Неймана —     Квантовая механика …   Википедия

  • Уравнение Фоккера — Эволюция функции плотности вероятности согласно уравнению Фоккера  Планка. Уравнение Фоккера  Планка  одно из стохастических дифференциальных уравнений, описывает временную эволюцию функции плотности вероятности координат и… …   Википедия

  • ЛИУВИЛЛЯ ТЕОРЕМА — 1) Л. т. об ограниченных целых аналитических функциях: если целая функция f(z) комплексных переменных z=(z1 . . ., zn) ограничена, т. е. то f(z) есть константа. Это предложение, одно из основных в теории аналитич. функций, впервые, по видимому,… …   Математическая энциклопедия

  • Уравнение Боголюбова — Цепочка уравнений Боголюбова (цепочка ББГКИ, ББГКИ иерархия, цепочка уравнений Боголюбова  Борна  Грина  Кирквуда  Ивона)  система уравнений эволюции системы, состоящей из большого числа тождественных взаимодействующих частиц, заключенных в… …   Википедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»