ШТУРМА - ЛИУВИЛЛЯ УРАВНЕНИЕ

обыкновенное дифференциальное уравнение 2-го порядка вида

рассматриваемое на конечном или бесконечном интервале ( а, b)изменения переменном х, где р(х), l (х), r (х) - заданные коэффициенты, - комплексный параметр, a у - искомое решение. Если р(x),r (х) положительны и р(х)имеет первую производную, а р(х)r(х) - вторую производную, то с помощью подстановки Лиувилля (см. [1]) это уравнение сводится к стандартному виду

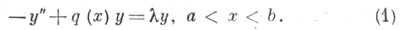
Предполагается, что комплексная функция q(x) измерима в интервале ( а, b) и суммируема в каждом его внутреннем подинтервале. Наряду с уравнением рассматривается также неоднородное уравнение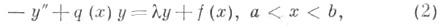

где f(x) - заданная функция.
Если функция f(x)измерима в интервале ( а, b) и суммируема в каждом его внутреннем подинтервале, то каковы бы ни были комплексные числа с ₀, с ₁ и какова бы ни была внутренняя точка х ₀ интервала ( а, b), уравнение (2) имеет в интервале ( а, b) одно и только одно решение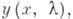 удовлетворяющее условиям 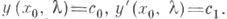Для каждого 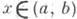функция 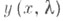является целой аналитич. цией В качестве точки х ₀ можно взять также и конечный конец интервала ( а, b )(если этот конец регулярен).
Пусть и 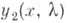- какие-нибудь два решения уравнения (1). Их вронскиан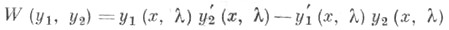

не зависит от хи равен нулю тогда и только тогда, когда эти решения линейно зависимы. Общее решение уравнения (2) представляется в виде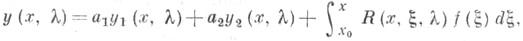

где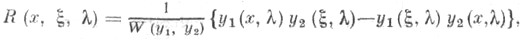

а ₁, а ₂ - произвольные постоянные, a - линейно независимые решения уравнения (1).
Справедлива следующая фундаментальная теорема Штурма (см. [1]): пусть даны два уравнения

.
если q₁(x), q₂ (х) действительны и q₁(x)<q₂(x)во всем интервале ( а, b), то между каждыми двумя нулями любого нетривиального решения первого уравнения заключен, по крайней мере, один нуль каждого решения второго уравнения.
Следующая теорема известна под названием теоремы сравнения (см. [1]): пусть левый конец интервала (a, b) конечен и и(х)есть решение уравнения (3), удовлетворяющее условиям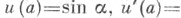 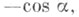а v(x) - решение уравнения (4) с теми же условиями; кроме того, пусть q₁(x)<q₂(x)во всем интервале ( а, b); тогда если и(х)в интервале ( а,b) имеет тнулей, то v(x)втом же интервале имеет не меньше m нулей и k-й нуль v(х)меньше k- гонуля и(х).
Одним из важных свойств уравнения (1) является существование для него так наз. операторов преобразования, имеющих простую структуру. Операторы преобразования возникли из общих алгебраич. соображений, связанных с теорией операторов обобщенного сдвига (преобразование базиса).
Для уравнения (1) существуют следующие типы операторов преобразования. Пусть - решение уравнения

удовлетворяющее условиям

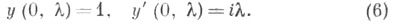
Оказывается, что это решение допускает представление

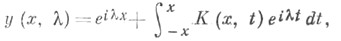
где К( х,t) - непрерывная не зависящая от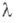 функция. причем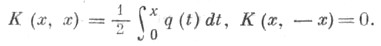

Интегральный оператор I+ К, определенный формулой

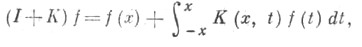
наз. оператором преобразования, сохраняющим условия в точке х=0. Он переводит функцию (решение простейшего уравнения -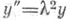 при условиях (6)) в решение уравнения (5) при тех же данных в точке х=0.
Пусть и - решения уравнения (5), удовлетворяющие условиям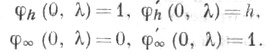

Эти решения допускают представления

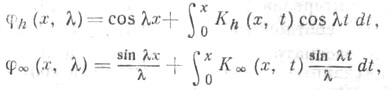
где и - непрерывные функции.
Введен (см.[8]|) новый вид операторов преобразования, сохраняющих асимптотику решений на бесконечности, а именно, оказалось, что для всех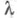 из верхней полуплоскости уравнение (5), рассматриваемое на полуоси 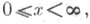при выполнении условия имеет решение представимое в виде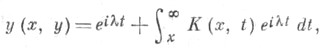

где функция К( х, t )является непрерывной и удовлетворяет неравенству

в к-ром

Кроме того,

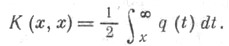
Лит.:[1] Левитан Б. М., Саргсян И. С., Введение в спектральную теорию, М., 1970; [2] Наймарк М. А., Линейные дифференциальные операторы, 2 изд., М., 1969; [3] Левитан Б. М., Теория операторов обобщенного сдвига, М., 1973; [4] Марченко В. А., Операторы Штурма- Лиувилля и их приложения, К., 1977; [5] Dе1sarte J., лС. r. Acad. sci.