ЛИНЕЙНОЕ ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ВТОРОГО ПОРЯДКА

обыкновенное - уравнение вида

где x(t) - искомая функция, a p(t), q(t).и r(t) - заданные функции, непрерывные на нек-ром промежутке (a, b). Для любых действительных чисел существует единственное решение x(t).уравнения (1) с начальными условиями причем x(t).определено для всех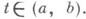

Если х ₁(t).и x₂(t) - линейно независимые решения соответствующего однородного уравнения

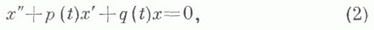
a x₀(t) - частное решение неоднородного уравнения (1), то общее решение уравнения (1) дается формулой

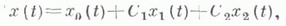
где C₁ и С ₂ - произвольные постоянные. Если известно одно ненулевое решение х ₁(t).уравнения (2), то второе его решение x₂(t), линейно ненависимое с x₁(t), дается формулой

Если известны линейно независимые решения x₁(t).и x₂(t) уравнения (2), то частное решение x₀(t).уравнения (1) можно найти методом произвольных постоянных вариации.

При изучении уравнения (2) большую роль играют его преобразования в уравнения других типов. Так, напр., заменой 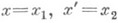уравнение (2) приводится к нормальной системе линейных уравнений 2-го порядка; заменой искомой функции

уравнение (2) приводится к уравнению

где

наз. инвариантом уравнения (2); заменой уравнение (2) сводится к Риккати уравнению

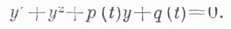
После умножения на

уравнение (2) принимает самосопряженный вид

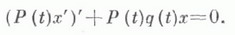
Уравнение (2) интегрируется в квадратурах лишь в отдельных случаях. Решения наиболее важных частных типов неинтегрируемых уравнений (2) входят в число специальных функций.

Справедлива теорема Штурма о разделении нулей: если x₁(t), x₂(t) - линейно независимые решения уравнения (2) и t₁<t₂ - соседние нули решения х ₁(1), то на интервале (t₁, t₂) имеется в точности один нуль решения х ₂(t).

Пусть в уравнениях

функции q₁ и q₂ непрерывны и q₂(t)>q₁(t).на промежутке (a, b). Справедлива теорема сравнения: если t₁<t₂ - последовательные нули ненулевого решения первого уравнения (3), то на интервале (t₁, t₂) имеется хотя бы один нуль любого решения второго уравнения (3).

Линейная краевая задача для уравнения (1) ставится следующим образом: найти решение x(t).уравнения (1), удовлетворяющее краевым условиям

где.

- заданные постоянные и

Штурма - Лиувилля задача для уравнения

где q(t)>0 и непрерывна на [ а, b], ставится следующим образом: найти те значения параметра при к-рых это уравнение имеет ненулевое решение x(t), удовлетворяющее краевым условиям х(а)=х(b)=0. Эти значения наз. собственными значениями, а соответствующие решения - собственными функциями.

Если в уравнении (2) t и x комплексны, а функции p(t).и q(t).голоморфны в точке t₀, то для любых чисел существует единственное голоморфное в точке t₀ комплексное решение x(t).уравнения (2), удовлетворяющее начальным условиям Если в уравнении

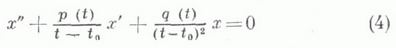
функции р(t).и q(t).голоморфны в точке t₀, причем хотя бы одно из чисел 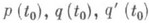отлично от нуля, то точка t₀ наз. регулярной особой точкой для уравнения (4). В окрестности такой точки решение уравнения (4) отыскивается в виде обобщенного степенного ряда

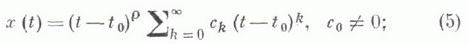
здесь 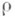находится из определяющего уравнения

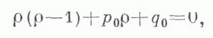
где p₀=p(t₀) и q₀=q(t₀). Пусть корни 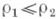этого уравнения действительны. Если не является целым, то существуют два линейно независимых решения вида (5): при и при Если 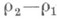- целое, то, вообще говоря, существует лишь одно решение в виде (5) при 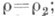второе решение имеет более сложный вид (см. [3]-[6]).

Лит.:[1] Понтрягин Л. С., Обыкновенные дифференциальные уравнения, 3 изд., М., 1970; [2] Камке Э.,Справоч-

ник по обыкновенным дифференциальным уравнениям, пер. с нем., 5 изд., М., 1976; [3] Сансоне Д ж., Обыкновенные дифференциальные уравнения, пер. с итал., т. 1-2, М., 1953- 1954; [4] Хартман Ф., Обыкновенные дифференциальные уравнения, пер. с англ., М., 1970; [5] Т р и к о м и Ф., Дифференциальные уравнения, пер. с англ., М., 1962; [6] Голубев В. В., Лекции по аналитической теории дифференциальных уравнений, 2 изд., М.- Л., 1950. Н. Н. Ладис.