- ЛЕРЕ ФОРМУЛА
Кош и - Фантапье формула,- формула интегрального представления голоморфных функций f(z) многих комплексных переменных
обобщающая интегральную формулу Коши (см. Коши интеграл).
Пусть D- конечная область комплексного пространства
с кусочно гладкой границей дD;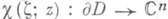 
- любая гладкая вектор-функция от 
со значениями в 
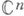такая, что скалярное произведение
всюду на дD для всех
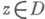. Тогда любая голоморфная в Dфункция f(z), непрерывная в замкнутой области 
представима в виде
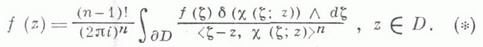
Формула (*) обобщает классическую интегральную формулу Коши для аналитич. функций одного комплексного переменного и наз. формулой Лере. Ж. Лере (J. Leray), получивший эту формулу (см. [1]), назвал ее формулой Коши - Фантапье. В этой фор-
муле дифференциальные формы
и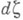 
составляются по законам:
где
- знак внешнего умножения (см. Внешнее произведение). Выбирая вид функции 
из формулы (*) можно получить различные интегральные представления. При этом следует иметь в виду, что, вообще говоря, интеграл Лере в формуле (*) не равен тождественно нулю, когда z находится вне D.
См. также Бохнера - Мартинелли представление. Лит.:[1] Лере Ж., Дифференциальное и интегральное исчисление на комплексном аналитическом многообразии, пер. с франц., М., 1961; [2] Ш а б а т Б. В., Введение в комплексный анализ, 2 изд., ч. 2, М., 1976. Е. Д. Соломенцев.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
