ЛЕБЕГА ИНТЕГРАЛ

- одно из наиболее важных обобщений понятия интеграла. Пусть 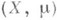- пространство с неотрицательной полной счетноаддитивной мерой 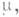причем 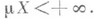Простой ф у. н к ц и е й наз. измеримая функция 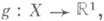принимающая не более счетного множества значений: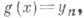 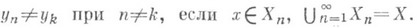Простая функция gназ. суммируемой, если ряд

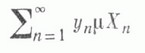
сходится абсолютно; сумма этого ряда есть интеграл Лебега:

Функция 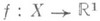суммируема на 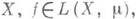если существует равномерно сходящаяся на множестве полной меры к f последовательность простых суммируемых функций g_n и предел

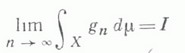
конечен. Число I есть интеграл Лебега:

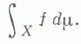
Определение корректно: предел I существует и не зависит от выбора последовательности g_n. Если то I - измеримая почти всюду конечная функция на X. Л. и. есть линейный неотрицательный функционал на обладающий следующими свойствами:

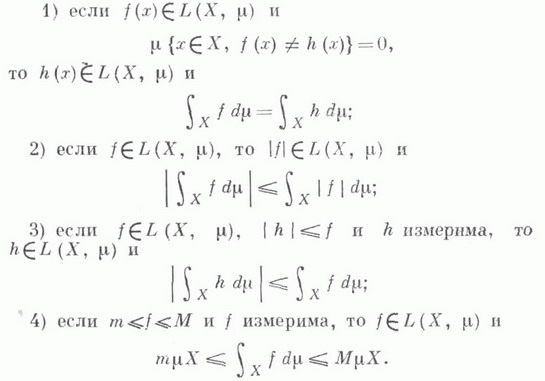
В случае, когда

интеграл Лебега

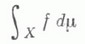
определяется как

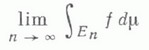
при условии, что этот предел существует и конечен для любой последовательности Е _п такой, что

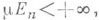
В этом случае свойства 1), 2), 3) сохраняются, а свойство 4) нарушается. О переходе к пределу под знаком Л. и. см. Лебега теорема. Если Аесть измеримое множество X, то Л. и.

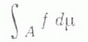
определяется или, как указано выше, заменой Xна А , или как

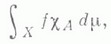
где - характеристич. функция А;эти определения

эквивалентны. Если 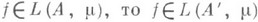для

любого измеримого Если

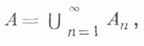
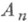измеримо для каждого п, для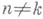

Обратно, если при тех же условиях на А _n для каждого 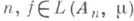и

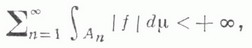
то 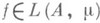и верно предыдущее равенство ( 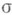-аддитивность Л. и.).

Функция множества

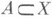
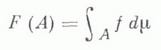
абсолютно непрерывна относительно 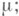если 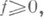то F(А).есть неотрицательная абсолютно непрерывная относительно 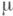мера. Обратное утверждение представляет Радона - Никодима теорему.

Для функций 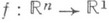название "интеграл Лебега" применяется к соответствующему функционалу, если мера 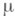есть Лебега мера;при этом множество суммируемых функций обозначается просто L(Х).и интеграл

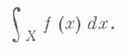
Для других мер этот функционал наз. Лебега-Стилтьеса интегралом.

Если 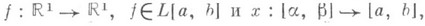- неубывающая абсолютно непрерывная функция, то

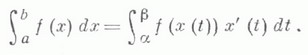
Если

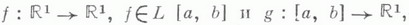
-мо-

нотонна на

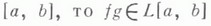
и существует точка

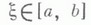
такая, что

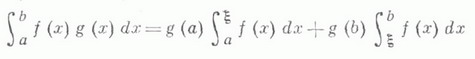
(вторая теорема о среднем).

А. Лебег дал в 1902 (см. [1]) определение интеграла для 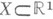и меры являющейся мерой Лебега. Он строил простые функции, равномерно приближающие почти всюду на множестве конечной меры Еизмеримую неотрицательную функцию 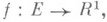и доказал существование общего предела (конечного или бесконечного) интегралов этих простых функций при стремлении их к f. Л. и. является базой для различных обобщений понятия интеграла. Как отметил Н. Н. Лузин [2], свойство 2) - т. н. абсолютная интегрируемость, выделяет Л. к. для из всевозможных обобщенных интегралов.

Лит.:[1] Лебег А., Интегрирование и отыскание примитивных функций, пер. с франц., М.- Л., 1934; [2] Лузин Н. Н., Интеграл и тригонометрический ряд, М.- Л., 1951; [3] Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 5 изд., М., 1981. И. А. Виноградова.