АЛГЕБРАИЧЕСКОЕ ЧИСЛО

Ч комплексное (в частности, действительное) число, являющееся корнем многочлена

с рациональными коэффициентами, из к-рых не все равны нулю. Если Ч А. ч., то среди всех многочленов с рациональными коэффициентами, имеющих своим корнем, существует единственный многочлен наименьшей степени со старшим коэффициентом, равным 1, и, следовательно, неприводимый (см. Неприводимый многочлен). Он наз. каноническим, или минимальным, многочленом А. ч.. Степень пканонич. многочлена наз. степенью А. ч.. Существование неприводимых многочленов любой степени побусловливает существование А. ч. степени п. Все рациональные числа, и только они, являются А. ч. 1-й степени. Число г есть А. ч. 2-й степени как корень многочлена при любом натуральном песть А. ч. степени пкак корень неприводимого многочлена .

Корни а _х, . . ., аД канонич. многочлена наз. числами» сопряженными с А. ч.,и тоже являются А. ч-степени п. Все числа, сопряженные с , различны-■ Важной характеристикой А. ч., кроме степени, является его высота (аналог знаменателя рациональной дроби). Высотой А. ч. наз. наибольшая из абсолютных величин коэффициентов в неприводимом и примитивном многочлене с целыми рациональными коэффициентами, имеющем своим корнем. Сумма, разность, произведение и частное двух А. ч. (кроме деления на нуль) суть А. ч., т. е. множество всех А. ч. образует поле. Корень многочлена с алгебраич. коэффициентами есть А. ч.

А. ч. наз. целым, если все коэффициенты в его канонич. многочлене Ч целые рациональные числа. Напр., 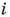и 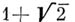Ч целые А. ч. как корни многочленов и .

Понятие целого А. ч. является обобщением понятия целого рационального числа (целое рациональное число есть целое А. ч. как корень многочлена ). Многие свойства целых рациональных чисел сохраняются и для целых А. ч. Так, целые А. ч. образуют кольцо. Однако действительные целые А. ч. образуют всюду плотное множество, в то время как целые рациональные Ч дискретное множество. В 1872 Г. Кантор (G. Kantor) доказал, что множество всех А. ч. счетно, откуда следовало существование трансцендентных чисел.

Корень любого (не обязательно неприводимого) многочлена с целыми рациональными коэффициентами и старшим коэффициентом, равным единице, является целым А. ч. Более того, корень многочлена с целыми алгебраич. коэффициентами и старшим коэффициентом 1 есть целое А. ч. В частности, корень любой степени киз целого А. ч. есть целое А. ч. Для всякого А. ч. существует такое натуральное , что Ч целое А. ч. (аналогия с рациональными числами). В качестве наименьшего возможного числа 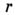можно взять модуль старшего коэффициента в неприводимом и примитивном многочлене с целыми рациональными коэффициентами, имеющем своим корнем. Все сопряженные целого А. ч. <Ч тоже целые А. ч.

Говорят, что целое А. ч. делится на целое А. ч. , если существует целое А. ч. , для к-рого . Для целых А. ч. справедливы многие свойства делимости, к-рые имеют место для целых рациональных чисел.

Целое А. ч. наз. алгебраич. единицей (коротко Ч единицей), если оно делит число 1, т. е. если Ч целое А. ч. Единица делит любое целое А. ч. Число, обратное единице, есть единица; числа, сопряженные с единицей, суть единицы; каждый делитель единицы есть единица; произведение конечного числа единиц есть единица. Целое А. ч. будет единицей тогда и только тогда, когда произведение всех его сопряженных равно . Корни k-й степени из числа 1 являются единицами, причем каждая из них по модулю равна 1. Существует бесконечное множество других единиц, не равных по модулю 1. Напр., числа и являются единицами как корни многочлена . Но среди их степеней найдутся единицы, сколь угодно малые и сколь угодно большие по величине. В поле рациональных чисел имеются лишь две единицы

Два целых А. ч. наз. ассоциированными, если они отличаются множителем, являющимся единицей. Имеется еще одно важное отличие кольца целых А. ч. от кольца целых рациональных чисел. В первом Ч нельзя ввести понятие неразложимого целого числа (аналог простого числа). Это видно хотя бы из того, что корень из любого целого А. ч. есть целое А. ч. Понятие неразложимого числа (с точностью до класса ассоциированных чисел) можно ввести в нек-рых подполях поля всех А. ч., так наз. алгебраических полях. Но оказывается, что в таких полях разложение целого А. ч. на неразложимые сомножители не всегда однозначно.

А. ч. не допускают слишком хорошее приближение рациональными и алгебраич. числами (теорема Лиувил-ля). Этот факт впервые позволил в 1844 доказать существование трансцендентных чисел. Проблема приближения А. ч. рациональными является одной из труднейших в теории чисел; в ее решении получены очень важные результаты (теоремы Туэ, ТуэЧЗигеля, Туэ Ч Зигеля Ч Рота), но она еще далека от окончательного завершения. Другой труднейшей проблемой теории чисел является вопрос о разложении А. ч. в цепные дроби. Действительные А. ч. 2-й степени (квадратичные иррациональности) представляются в виде бесконечных периодических цепных дробей. О характере разложения действительных А. ч. степеней выше 3-й в обыкновенные цепные дроби до сих пор (70-е гг. 20 в.) ничего не известно.

Комплексное число наз. алгебраическим числом над полем Р, если оно является корнем многочлена (1) с коэффициентами из Р. Для А. ч. над полем Р аналогично определяются канонич. многочлен, степень над полем Р, сопряженные числа над полем Р. Корень многочлена, коэффициенты к-рого Ч алгебраические числа над Р, есть А. ч. над Р.

Не над любым полем Рмогут существовать А. ч. любой степени п. Напр., над полем комплексных чисел существуют только А. ч.1-й степени Ч сами числа этого поля. Одно и то же А. ч. может относительно различных полей иметь разные степени. Так, число iявляется А. ч. 2-й степени, но имеет 1-ю степень относительно поля комплексных чисел. Множество всех А. ч. над полем Робразует числовое поле.

Впервые А. ч. и алгебраич. поле систематически стал рассматривать К. Гаусс (С. Gauss) (гауссовы числа вида , где аи b Ч рациональные числа). Для обоснования теории биквадратичных вычетов он развил арифметику целых гауссовых чисел. Изучая теорию кубических вычетов, К. Якоби (С. Jacobi) и Ф. Эйзенштейн (F. Eisenstein) создали арифметику чисел вида , где - кубич. корень из числа 1, а аи b Ч рациональные числа. Попытки доказать Ферма теорему привели Э. Куммера (Е. Kummer) к глубокому изучению полей деления круга (см. Круговое поле), введению понятия идеала и созданию элементов теории А. ч. В работах П. Дирихле (P. Dirichlet), Л. Кронекера (L. Kronecker), Д. Гильберта (D. Hilbert) и др. теория А. ч. получила свое дальнейшее развитие. Большой вклад в нее внесли русские математики Е. И. Золотарев (теория идеалов), Г. Ф. Вороной (кубич. иррациональности, единицы кубич. полей), А. А. Марков (кубич. поле), Ю. В. Сохоцкий (теория идеалов) и др.

Понятие А. ч. и связанное с ним понятие алгебраич. поля Ч важнейшие понятия теории чисел и алгебры. А. ч., являясь обобщением рациональных чисел, выделяют в полях действительных и комплексных чисел подполя А. ч., обладающих специальными алгебраич. свойствами. Развитие теории А. ч. оказало большое влияние на создание и развитие общей теории колец и полей.

А. ч. находит большое применение в различных разделах теории чисел, алгебры и др. разделах математики:

теории форм, диофантовых уравнениях, диофантовых приближениях, трансцендентных числах, геометрии чисел, алгебраической геометрии, теории Галуа и др. Лит.: [1] Чеботарев Н. Г., Основы теории Галуа, ч. 1Ч2, М. <Ч Л., 1934Ч37; [2] Гекке Э., Лекции по теории алгебраических чисел, пер. с нем., М. <Ч Л., 1940; [3] Landau Е., Einfuhrung in die elementare und analytische Theorie der algebraischen Zahlen und der Ideale, Lpz.ЧВ., 1918; [4] Landau E., Vorlesungen iiber ZahJentheorie, Bd 3, Lpz., 1927; [5] Ленг С, Алгебраические числа, пер. с англ., М., 1966.

А. Б. Шидловский.