- КОНФОРМНЫХ ОТОБРАЖЕНИИ ГРАНИЧНЫЕ СВОЙСТВА
- свойства функций, конформно отображающих одну область комплексной плоскости на другую, проявляющиеся вблизи границы отображаемой области и на самой границе. К числу таких свойств относятся: возможность непрерывного продолжения функции w=f(z), конформно отображающей рассматриваемую область G, на область G2, в нек-рую точку Z, границы Т 1 области G1 или на всю границу Г 1 этой области; характер разрыва в случае невозможности такого продолжения; наличие конформности продолженного отображения в граничных точках
 дифференциально-гладкостные свойства продолженной функции на Г 1 и на замкнутой области
дифференциально-гладкостные свойства продолженной функции на Г 1 и на замкнутой области  принадлежность производной /' (z),
принадлежность производной /' (z),  отображающей функции к различным классам функций, аналитических в G1, и т. п. Эти свойства изучаются в зависимости от свойств границ областей G1 и G2. Из самых общих К. о. г. с. можно выделить следующее: каковы бы ни были односвязные области G1 и G2 и однолистное конформное отображение w=f(z)области G1 на G2, это отображение устанавливает взаимно однозначное соответствие между граничными элементами этих областей в том смысле, что класс всех эквивалентных путей, лежащих в области G1 и определяющих нек-рый граничный элемент z области G1, переходит при этом отображении в класс всех эквивалентных путей, лежащих в области G2 и определяющих нек-рый граничный элемент со области G2 (обратное отображение z=f-1(w),
отображающей функции к различным классам функций, аналитических в G1, и т. п. Эти свойства изучаются в зависимости от свойств границ областей G1 и G2. Из самых общих К. о. г. с. можно выделить следующее: каковы бы ни были односвязные области G1 и G2 и однолистное конформное отображение w=f(z)области G1 на G2, это отображение устанавливает взаимно однозначное соответствие между граничными элементами этих областей в том смысле, что класс всех эквивалентных путей, лежащих в области G1 и определяющих нек-рый граничный элемент z области G1, переходит при этом отображении в класс всех эквивалентных путей, лежащих в области G2 и определяющих нек-рый граничный элемент со области G2 (обратное отображение z=f-1(w), переводит класс эквивалентных путей, определяющих со, в класс эквивалентных путей, определяющих z). При этом в специальной топологии f задает гомеоморфизм области G2 с присоединенными ее граничными элементами (рассматриваемыми наряду с точками
переводит класс эквивалентных путей, определяющих со, в класс эквивалентных путей, определяющих z). При этом в специальной топологии f задает гомеоморфизм области G2 с присоединенными ее граничными элементами (рассматриваемыми наряду с точками  как точки топологич., пространства) на область G2 с присоединенными граничными элементами. Обычно рассматривается случай, когда одна из областей G1,G2 является единичным кругом D= {z: |z|<1} (реже полуплоскостью или углом), общий же случай сводится к этому частному случаю.
как точки топологич., пространства) на область G2 с присоединенными граничными элементами. Обычно рассматривается случай, когда одна из областей G1,G2 является единичным кругом D= {z: |z|<1} (реже полуплоскостью или углом), общий же случай сводится к этому частному случаю.Пусть w=f(z)- однолистное конформное отображение круга Dс границей С= {z:|z| = l} на ограниченную односвязную область G с границей Г, z=j(w)- обратное конформное отображение: cp(/(z)) = z при
 Имеют место следующие результаты.
Имеют место следующие результаты.1) Для того чтобы отображение w=f(z)непрерывно продолжалось в точку
 необходимо и достаточно, чтобы граничный элемент области G, соответствующий точке z при этом отображении, был граничным элементом 1 рода (т. е. состоял из единственной точки). Для непрерывной продолжимости функции z=j(w) в точку
необходимо и достаточно, чтобы граничный элемент области G, соответствующий точке z при этом отображении, был граничным элементом 1 рода (т. е. состоял из единственной точки). Для непрерывной продолжимости функции z=j(w) в точку 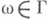 необходимо и достаточно, чтобы со входила в состав лишь одного граничного элемента (точнее, в состав лишь одного носителя граничного элемента области G). Если Г - замкнутая жорданова кривая, то fнепрерывно продолжается на С, а j - на Г, так что продолженные функции осуществляют взаимно однозначное и взаимно непрерывное отображение (гомеоморфизм) замкнутых областей
необходимо и достаточно, чтобы со входила в состав лишь одного граничного элемента (точнее, в состав лишь одного носителя граничного элемента области G). Если Г - замкнутая жорданова кривая, то fнепрерывно продолжается на С, а j - на Г, так что продолженные функции осуществляют взаимно однозначное и взаимно непрерывное отображение (гомеоморфизм) замкнутых областей 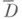 и
и  друг на друга.
друг на друга.Всюду ниже Г обозначает жорданову кривую и предполагается, что функции f и j уже продолжены по непрерывности на С и Г соответственно.
2) Если Г - замкнутая жорданова спрямляемая кривая, то граничные функции f(z),
 и j(w)),
и j(w)),  являются абсолютно непрерывными. Таким образом, отображения w=f(z),
являются абсолютно непрерывными. Таким образом, отображения w=f(z),  и z=j(w),
и z=j(w), переводят граничные множества меры нуль в граничные множества меры нуль. Функция f(z)имеет конечную ненулевую производную относительно замкнутого круга Dпочти в каждой точке
переводят граничные множества меры нуль в граничные множества меры нуль. Функция f(z)имеет конечную ненулевую производную относительно замкнутого круга Dпочти в каждой точке  а функция j(w) имеет конечную ненулевую производную почти в каждой точке
а функция j(w) имеет конечную ненулевую производную почти в каждой точке  Следовательно, эти отображения обладают свойством конформности (т. е. свойством постоянства растяжений и сохранения углов) почти в каждой граничной точке соответствующей области. Функция f' (z) принадлежит классу Харди Н 1.
Следовательно, эти отображения обладают свойством конформности (т. е. свойством постоянства растяжений и сохранения углов) почти в каждой граничной точке соответствующей области. Функция f' (z) принадлежит классу Харди Н 1.3) Пусть Г - спрямляемая жорданова замкнутая кривая со свойством: для любой пары различных точек
 отношение длины меньшей из дуг, на к-рые эти точки разбивают кривую Г, к расстоянию |w1-w2| между этими точками ограничено сверху некрой величиной d, не зависящей от w1. и w2. Тогда функция f(z) удовлетворяет на
отношение длины меньшей из дуг, на к-рые эти точки разбивают кривую Г, к расстоянию |w1-w2| между этими точками ограничено сверху некрой величиной d, не зависящей от w1. и w2. Тогда функция f(z) удовлетворяет на 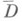 условию Гёльдера порядка 2(1+d)-2.
условию Гёльдера порядка 2(1+d)-2.4) Пусть Г - гладкая замкнутая жорданова кривая. Зафиксируем нек-рую точку
 и при
и при 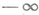 <s<
<s< отложим вдоль Г дугу длины |s| в положительном (при s>0) или отрицательном (при s<0) направлении обхода области G. Пусть со (s) - конец отложенной дуги, a t(s).- угол между положительным направлением действительной оси и положительным направлением касательной в точке w(s) (значение угла t(s) выбирается так, чтобы функция t(s). была непрерывной). Если при нек-ром р=0, 1, ... существует производная t(p)>(s), удовлетворяющая условию Гёльдера нек-рого положительного порядка a<1, то функция f(p+1)(z) непрерывна и удовлетворяет условию Гёльдера того же порядка a. на замкнутом круге
отложим вдоль Г дугу длины |s| в положительном (при s>0) или отрицательном (при s<0) направлении обхода области G. Пусть со (s) - конец отложенной дуги, a t(s).- угол между положительным направлением действительной оси и положительным направлением касательной в точке w(s) (значение угла t(s) выбирается так, чтобы функция t(s). была непрерывной). Если при нек-ром р=0, 1, ... существует производная t(p)>(s), удовлетворяющая условию Гёльдера нек-рого положительного порядка a<1, то функция f(p+1)(z) непрерывна и удовлетворяет условию Гёльдера того же порядка a. на замкнутом круге 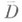 и
и 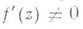 на
на  а <j(p+1)(w) непрерывна и удовлетворяет условию Гёльдера порядка а на
а <j(p+1)(w) непрерывна и удовлетворяет условию Гёльдера порядка а на  и
и  на G.
на G.Лит.:[1] Маркушевич А. И., Теория аналитических функций, 2 изд., т. 2, М., 1968; [2] Коллингвуд Э., Ловатер А., Теория предельных множеств, пер. с англ., М., 1971; [3] Привалов И. И., Граничные свойства аналитических функций, 2 изд., М.- Л., 1950; [4] Голузин Г. М., Геометрическая теория функций комплексного переменного, 2 изд., М., 1966; [5] Warsсhawski S. E., "Proc. Amer. Math. Soc", 1961, v. 12, № 4, p. 614-20; [6] Kellogg O. D., "Trans. Amer. Math. Soc", 1912, v. 13, № 1, p. 109-32; [7] Долженко Е. П., "Изв. АН СССР. Сер. матем.", 1965, т. 29, с. 1069-84.
Е. <П. Долженко.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
