- КВАЗИКОНФОРМНОЕ ОТОБРАЖЕНИЕ
- отображение с ограниченным искажением или ограниченным отклонением от конформного. Числовой характеристикой искажения при отображении f :
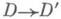 в точке
в точке  является коэффициент k(f, а )квазиконформности (или дилатация) отображения f в этой точке:
является коэффициент k(f, а )квазиконформности (или дилатация) отображения f в этой точке: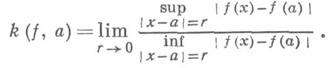
Величина
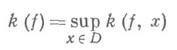 наз. коэффициентом квазиконформности (или дилатацией) отображения f в области D. Сохраняющее ориентацию отображение f :
наз. коэффициентом квазиконформности (или дилатацией) отображения f в области D. Сохраняющее ориентацию отображение f :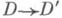 наз. квазиконформным (или отображением с ограниченным искажение м), если
наз. квазиконформным (или отображением с ограниченным искажение м), если 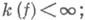 оно наз. k-к вазиконформным, если
оно наз. k-к вазиконформным, если  Для конформного отображения k(f) = k(f, x)=1. Если f дифференцируемо в точке
Для конформного отображения k(f) = k(f, x)=1. Если f дифференцируемо в точке  то линейное отображение f' (а)преобразует шар касательного пространства в эллипсоид, отношением наибольшей полуоси к-рого к наименьшей будет k(f, а). Наряду с данным определением часто используются следующие эквивалентные ему условия квазиконформности f в области
то линейное отображение f' (а)преобразует шар касательного пространства в эллипсоид, отношением наибольшей полуоси к-рого к наименьшей будет k(f, а). Наряду с данным определением часто используются следующие эквивалентные ему условия квазиконформности f в области 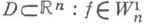 (т. е. f имеет обобщенные производные, локально суммируемые в Dв степени п)и существует такое действительное число k, что
(т. е. f имеет обобщенные производные, локально суммируемые в Dв степени п)и существует такое действительное число k, что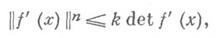
или

почти во всех точках

Термин "К. о.", как правило, предполагает гомеоморфность отображения. Негомеоморфные отображения с ограниченным искажением обычно наз. квазирегулярными. Теория К. о. областей в Rn при п=2 и
 если не считать общих для них и, как правило, более простых вопросов, имеет- ярко выраженную специфику.
если не считать общих для них и, как правило, более простых вопросов, имеет- ярко выраженную специфику.Двумерная теория. В этом случае дифференциал отображения в точке
 может быть записан в виде
может быть записан в виде 
С точностью до множителя он определяется соотношением
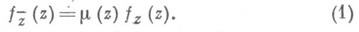
Функция m(z) наз. комплексной характеристикой отображения /в точке z; |m(z)|<1 для отображений с положительным якобианом J= |fz|2-|fz-|2. Для аналитич. отображений m(z)=0- условия Коши - Римана. Коэффициент k(f, z)квазиконформности отображения в точке выражается через m(z). в виде
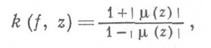 поэтому условие квазиконформности отображения f
поэтому условие квазиконформности отображения f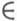 W12 в терминах комплексной характеристики есть
W12 в терминах комплексной характеристики естьОбычно соотношение (1) появляется как уравнение относительно f при известной функции m; оно наз. уравнением (или системой) Бельтрами. Напр., задача конформного отображения одной области Dна другую D' есть задача отыскания гомеоморфизма f:
 удовлетворяющего в Dуравнению Бельтрами с
удовлетворяющего в Dуравнению Бельтрами с 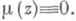
К решению общего уравнения (1) сводится, напр., классич. задача об одновременном во всей области Dприведении к канонич. виду заданной в Dположительно определенной квадратичной формы от двух переменных или, что то же самое, задача построения конформно евклидовых координат на двумерной поверхности (см. [2]).
Основной факт двумерной теории К. о., аналогичный Римана теореме для конформных отображений, состоит в следующем: для всякой измеримой в области
 функции m(z) такой, что
функции m(z) такой, что 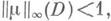 найдется квазиконформный гомеоморфизм f области Dс комплексной характеристикой m(z);. общее решение уравнения (1) в области Dимеет вид Fof(z), где f - построенный квазиконформный гомеоморфизм, a F- любая аналитич. функция.
найдется квазиконформный гомеоморфизм f области Dс комплексной характеристикой m(z);. общее решение уравнения (1) в области Dимеет вид Fof(z), где f - построенный квазиконформный гомеоморфизм, a F- любая аналитич. функция.Если D- единичный круг, то f можно выбрать так, что f(D)=D. Тогда f продолжается до гомеоморфизма замкнутого круга на себя и условия нормировки f(0)=0, f(1)=1 выделяют единственный гомеоморфизм/ :
 удовлетворяющий уравнению Бельтрами. Если, кроме того,
удовлетворяющий уравнению Бельтрами. Если, кроме того, 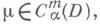 0<a<1,
0<a<1, 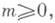 то
то 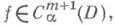 где
где  - пространство функций, имеющих в D т непрерывных производных, причем последняя удовлетворяет в Dусловию Гёльдера с показателем a. Если последовательность fn нормированных квазиконформных автоморфизмов круга Dтакова, что
- пространство функций, имеющих в D т непрерывных производных, причем последняя удовлетворяет в Dусловию Гёльдера с показателем a. Если последовательность fn нормированных квазиконформных автоморфизмов круга Dтакова, что 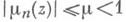 и
и при
при 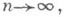 то
то
К. о. как гомеоморфные решения сильно эллиптических систем

так же естественно связаны с проблемами струйных течений дозвуковой газовой динамики, как конформные отображения, удовлетворяя системе Коши - Римана, связаны с течением несжимаемой идеальной жидкости (см. [1], [5]).
Общая задача построения К. о. одной односвязной области на другую, удовлетворяющего системе (2), была поставлена и решена М. А. Лаврентьевым [1] - одним из основателей теории К. о. В явном виде понятие К. о. появилось у X. Грётша (Н. Grotzsch, см. [3]) в связи со следующей экстремальной задачей (задачей Грётша): среди отображений с соответствием вершин квадрата на прямоугольник, не являющийся квадратом, найти наиболее близкое к конформному. Чтобы охарактеризовать меру этой близости, пришлось ввести коэффициент квазиконформности - начальное понятие геометрич. теории К. о.
В двумерной теории К. о., как и в теории аналитич. функций, исследованы общие вопросы компактности - нормальности семейства отображений; построена теория соответствия границ; показавшая, что это соответствие осуществляется по тем же простым концам в смысле Каратеодори (см. Граничные элементы), как и в конформном случае; изучены условия устранимости множества особенностей; разработаны вариационные принципы решения основных экстремальных задач на классе квазиконформных гомеоморфизмов (см. [4], [7]).
Важное применение в геометрич. теории функций двумерные К. о. получили в исследованиях по проблеме модулей римановых поверхностей в связи с Тайхмюллера пространством и деформацией клейновых групп (см.
Пространственная теория. Теория К. о. областей пространства
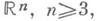 также имеет свою специфику. Прежде всего это связано с отсутствием конформных отображений: по теореме Лиувилля всякое достаточно гладкое конформное отображение области
также имеет свою специфику. Прежде всего это связано с отсутствием конформных отображений: по теореме Лиувилля всякое достаточно гладкое конформное отображение области 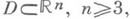 является мёбиусовым, т. е. суперпозицией инверсий и вращений. Суть этого факта в том, что условия конформности отображения при
является мёбиусовым, т. е. суперпозицией инверсий и вращений. Суть этого факта в том, что условия конформности отображения при  в отличие от условий Коши - Римана при n=2, составляют переопределенную систему уравнений с частными производными.
в отличие от условий Коши - Римана при n=2, составляют переопределенную систему уравнений с частными производными.Ниже указаны нек-рые важные результаты пространственной теории К. о. Теорема Лиувилля остается в силе как в случае гильбертова пространства, так и при минимальных априорных условиях регулярности отображения. В теореме Лиувилля имеет место устойчивость в том смысле, что существуют константы k1 и k2 и функция l(e)=О(e)при
 обладающие следующими свойствами: а) если y=f(x)есть К. о. шара | х|<1c k(f)<k1 то существует мёбиусово отображение L(y)такое, что
обладающие следующими свойствами: а) если y=f(x)есть К. о. шара | х|<1c k(f)<k1 то существует мёбиусово отображение L(y)такое, что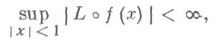
и образ единичного шара при отображении Lof содержит шар |y|<1; б) если
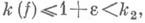 то
то
где

в) если
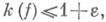 то
то
во всем шаре |x|<1. Устойчивость имеет место также в нек-рых классах областей с нерегулярной границей. Подобно тому, как 1-квазиконформное отображение оказывается мёбиусовым даже без априорного предположения гомеоморфности, К. о. локально гомеоморфно как только его коэффициент квазиконформности достаточно близок к 1. В отличие от плоского случая, всякое локально гомеоморфное К. о. единичного шара в Rn, n>3, автоматически гомеоморфно в нек-ром шаре | х|<r(n, k)<1, где rзависит только от размерности ппространства и коэффициента квазиконформности k=k(f)отображения. В частности, локально гомеоморфное К. о. всего пространства Rn, п>3, глобально гомеоморфно и f(Rn)=Rn.
Граничное поведение: если f :
 есть К. о, полупространства xn>0 пространства
есть К. о, полупространства xn>0 пространства  на себя, то fпродолжается до гомеоморфизма замкнутых областей; при этом индуцированный на границе
на себя, то fпродолжается до гомеоморфизма замкнутых областей; при этом индуцированный на границе 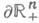 = Rn-1 гомеоморфизм j :
= Rn-1 гомеоморфизм j : в случае n=2 удовлетворяет M-условию;
в случае n=2 удовлетворяет M-условию;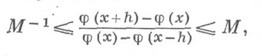
а в случае
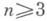 является квазиконформным. Каждое из последних двух условий в своей размерности не только необходимо, но и достаточно для того, чтобы отображение ф :
является квазиконформным. Каждое из последних двух условий в своей размерности не только необходимо, но и достаточно для того, чтобы отображение ф : было граничным следом нек-рого К. о. (при п -4 это пока (1978) не доказано).
было граничным следом нек-рого К. о. (при п -4 это пока (1978) не доказано).Вытекающая отсюда возможность продолжить квазиконформный автоморфизм пространства Лобачевского до К. о. абсолюта в совокупности с тем, что 1-квазиконформное отображение сферы конформно и является следом конформного автоморфизма шара, лежит в основе доказательства жесткости пространственных гиперболич. форм: если два замкнутых римановых многообразия размерности
 одной и той же постоянной отрицательной кривизны гомеоморфны, то они изометричны (см. [9]).
одной и той же постоянной отрицательной кривизны гомеоморфны, то они изометричны (см. [9]).Лит.:[1] Лаврентьев М. А., Вариационный метод в краевых задачах для систем уравнений эллиптического типа, М., 1962; [2] Векуа И. Н., Обобщенные аналитические функции, М., 1959; [3] Альфорс Л., Лекции по квазиконформным отображениям, пер. с англ., М., 1969; [4] Белинский П. П., Общие свойства квазиконформных отображений, Новосиб., 1974; [5] Берс Л., Математические вопросы дозвуковой и околозвуковой газовой динамики, пер. с англ., М., 1961; [6] Vaisa la Jussi, Lectures on "-dimensional quasieonformal mappings, В., 1971; [7] Крушкаль С. Л., Квазиконформные отображения и римановы поверхности, Новосиб., 1975; [8] Lento О., Virtanen К. I., Quasiconforme Abbildungen, В., 1965; [9] Мостов Г. Д., "Математика", 1972, т. 16, Mi 5, с. 105-57.
В. А. Зорин.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
