КОВАРИАНТНОЕ ДИФФЕРЕНЦИРОВАНИЕ

абсолютное дифференцирование, - операция, инвариантным образом определяющая понятия производной и дифференциала для полей геометрич. объектов на многообразиях - векторов, тензоров, форм и т. д. Основные понятия теории К. д. (под названием абсолютное дифференциальное исчисление) были даны в конце 19 в. в работах Г. Риччи (G. Ricci) и в наиболее полной форме изложены им в 1901 в совместной работе его с Т. Леви-Чивита (Т. Levi-Civita) (см. [1]). Сначала теория К. д. строилась на римановых многообразиях и предназначалась в первую очередь для исследования инвариантов дифференциальных форм. Впоследствии оказалось, что определение и свойства К. д. естественным образом связаны с введенными позже понятиями связности и параллельного перенесения на многообразиях, и теперь теория К. д. строится в общих рамках теории связностей. Как аппарат тензорного анализа, К. д. широко употребляется в теоретич. физике, особенно в общей теории относительности.

Пусть на n-мерном многообразии Мвведена аффинная связность и соответствующее параллельное перенесение векторов и вообще тензоров. Пусть X- гладкое векторное поле, и U- тензорное поле типа (r, s), т. е. г раз контравариантное и s раз ковариантное; ковариантной производной (относительно данной связности) тензорного поля Uв точке вдоль векторного поля Xназ. тензор того же типа (r, s)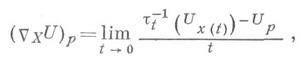

где x(t)- точка интегральной кривой у _х векторного поля Xс начальным условием x(0)=p, U _р и U_X(t)- локализации (значения) тензорного поля Uв точках ри x(t)соответственно, -результат параллельного перенесения тензора U_x(t) вдоль g_X из x(t)в р. Таким образом, основная идея определения ковариантной производной тензорного поля Uвдоль векторного поля Xзаключается в том, что ввиду отсутствия операций между тензорами U _р и U_x(t), принадлежащими разным слоям тензорного расслоения над М, т. е. принадлежащими тензорным пространствам Т ^r_s над разными касательными к Мплоскостями Т _р М и Т _х(t) М, в качестве "приращения" тензора Uрассматривается разность между и образом параллельно перенесенного в Т ^r_s( Т _р М )вдоль g_X тензора 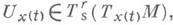и дальше, как обычно, берется предел отношения этого "приращения" к приращению аргумента t. В частности, если для точек x(t), близких к р, поле Uполучено параллельным перенесением тензора U _р вдоль g_X, то и тем самым в общем случае ковариантная производная поля Uв точке р вдоль Xопределяет начальную скорость отличия поля Uвдоль g_X от результата параллельного перенесения U _р вдоль g_X- Для тензорных полей нулевой валентности, т. е. для функций f из кольца дифференцируемых функций на М

что приводит к совпадению с производной fпо вектору X _р, т. е. с X_pf. При Х _р=0 для любого тензорного поля U, по определению, считается (С _XU)p=0. Введение ковариантной производной позволяет определить ковариантный дифференциал DU для тензорного поля Uвдоль гладкой кривой у(t)как и его можно рассматривать как главную линейную часть "приращения" тензора U(в описанном выше смысле) при перемещении точки вдоль уна бесконечно малый участок

Знание для тензорного поля Uтипа (r, s)в каждой точке вдоль каждого векторного поля X позволяет ввести два поля: 1) поле ковариантного дифференциала D U как тензорной 1-формы со значениями в модуле T^r_s(M), определенной на векторах Xпо формуле 2) поле ковариантной производной 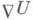как тензорного поля типа (r,s+1), канонически соответствующего форме DU и действующего на 1-формах wⁱ и векторах X;по формуле

Обычно под ковариантным дифференциалом понимается не сама 1-форма DU, а ее значения на векторах X, и в таком толковании (DU){X )тоже превращается в тензорное поле типа (r, s), локализация к-рого, в частности, при р = g(О) и Х=у совпадает с введенным выше ковариантным дифференциалом вдоль кривой y(t). Иногда ковариантная производная С U называется градиентом тензора U; а производная - ковариантным дифференциалом.

Если х'- локальные координаты,- базисные векторные поля, е ⁱ - сопряженные базисные 1-формы, Xⁱ и - координаты векторного и тензорного полей в этих базисах,- коэффициенты введенной на Маффинной связности, то, обозначая через или координаты тензорного поляСU, получают следующие выражения (для примера взяты r=2, s=l)

где - операция свертки по последним (третьему) контравариантному и (второму) ковариантному индексам.

Если М- аффинное пространство, х ⁱ- аффинные координаты, то является обычной производной тензорного поля Uпо векторному полю X,- частными производными Uв точке рпо х ^k,- обычным дифференциалом Uвдоль кривой y(t)и, таким образом, К. д. выступает как обобщение обычного дифференцирования с сохранением известных связей между частными производными и дифференциалами первого порядка.

Значение К. д. заключается в том, что оно дает удобный аналитический аппарат для изучения и записи свойств геометрич. объектов и операций в инвариантной форме. Напр., условие параллельного перенесения тензора Uвдоль кривой g. дается уравнением уравнение геодезической узаписывается в виде условие интегрируемости системы уравнений в ковариантных производных 1-го порядка сводится к нек-рому уравнению для альтернированной разности - внешнее дифференцирование форм на многообразии и в расслоениях над ним можно также выразить через К. д., и т. д.

Определение ковариантных производных высших порядков дается индуктивно:

Вообще говоря, получаемый при этом тензор 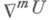не симметричен относительно последних ковариантных индексов; высшие ковариантные производные вдоль разных векторных полей также зависят от порядка дифференцирования. Альтернированные разности компонент ковариантных производных высших порядков выражаются через кривизны тензор Rⁱ_jkl и кручения тензор совместно характеризующих отличие многообразия Мс данной связностью от аффинного пространства. Напр.,

Определение К. д. и его свойства остаются в силе и в более общем случае, когда вместо сечения Uтензорного расслоения с аффинной связностью рассматривается сечение j произвольного (действительного или комплексного) векторного расслоения, ассоциированного нек-рому главному расслоению со связностью Г и со структурной группой G, к-рая действует на слое своим представлением в группе невырожденных матриц. Существуют определения К. д. в более общей ситуации, когда расслоение не обязательно является векторным; общий смысл [9] этих определений заключается в аналитическом выражении параллельного перенесения объекта или параллельности определяющего его сечения как равенства нулю результата К. д. Подобные подходы имеются и для бесконечномерных многообразий.

Лит.:[1] Riссi G., Levi-Civitа Т., "Math. Ann.", 1901, Bd 54, № 1, S. 125-201; [2] Pашевский IT. К., Риманова геометрия и тензорный анализ, М., 1967; [3] Нордев А. П., Пространства аффинной связности, 2 изд., М., 1976; [4] Лихнерович А., Теория связности в целом и группы голономий, пер. с франц., М., 1960; [5] Xелгасон С, Дифференциальная геометрия и симметрические пространства, пер. с англ., М., 1964; [6] Бишоп Р., Криттенден Р., Геометрия многообразий, пер. с англ., М., 1967; [7] Громол Д., Клингенберг В., Мейер В., Риманова геометрия в целом, пер. с нем., М., 1971; [8] Коbауashi S., Nоmizu K., Foundations of differential geometry, v. 1-2, N. Y.-L., 1963-69; [9] Итоги науки. Алгебра. Топйлогия. Геометрия. 1969, М., 1971,с. 123-68; [10] Зуланке Р., Винтген П., Дифференциальная геометрия и расслоения, пер. с нем., М., 1975.

И. X. Сабитов.