КВАЗИКЛАССИЧЕСКОЕ ПРИБЛИЖЕНИЕ

- асимптотическое представление, асимптотика решений уравнений квантовой механики при (h- постоянная Планка). Уравнение Шрёдингера

описывает движение квантовомеханич. частицы в потенциальном поле V(x). Движение классич. частицы описывается уравнением Гамильтона - Якоби

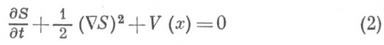
или системой Гамильтона

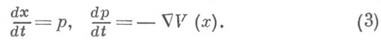
Задаче Коши для уравнения Шрёдингера

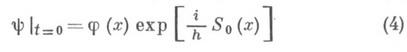
сопоставляется задача Коши для системы (3)

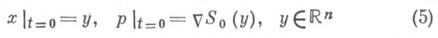
(здесь функции j, S₀, V- гладкие, S₀, V- действительные, j - финитна). Асимптотика решения y(t, x )при и при малых T>0 имеет вид: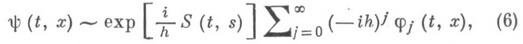

здесь S(t, x)- решение уравнения (2) с данными Коши S|_t=0=S₀(x)(классическое действие), а

где x=x(t, у), p=p(t, у) - решение задачи (3), (5). Функции j_j при 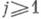определяются из рекуррентной системы уравнений переноса (это обыкновенные дифференциальные уравнения вдоль траекторий системы (3)), так что все члены асимптотики выражаются в терминах классич. механики. Принцип соответствия Бора утверждает: "Если hстремится к нулю, то квантовые законы должны переходить в законы классические". Метод отыскания асимптотики в виде (6) был предложен П. Дебаем (P. Debye) и широко применяется в квантовой механике.

Асимптотика решения задачи (1), (4) в большом (т. е. за любое конечное время) строится с помощью канонич. оператора В. П. Маслова [3]. Данные Коши (5) заполняют n-мерное лагранжево многообразие А" в фазовом пространстве Его сдвиги 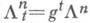вдоль траекторий системы (3) - также лагранжевы многообразия; их объединение 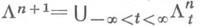есть (n+1)-мерное лагранжево многообразие в фазовом пространстве R²ⁿ⁺² с координатами (t, x, р ₀, р). Для канонич. оператора 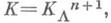отвечающего 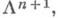справедлива формула коммутации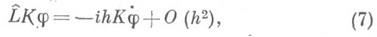

где 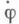- производная в силу системы (3), L- оператор Шрёдингера. Асимптотика решения y в большом дается формулой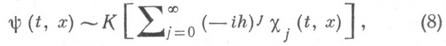

где функции c_j определяются из данных Коши (4) с помощью уравнений переноса и выражаются в терминах классич. механики. В нефокальной точке (t₀, x⁰ )асимптотика имеет вид

где сумма берется по всем лучам, приходящим в эту точку, S_j и J_j- действие и якобиан для j-го луча, l_j- индекс Морса j-го луча. Для стационарного уравнения Шрёдингера в К. п. исследованы задача о рассеянии, задача о поле точечного источника, получены квазиклассич. серии (типа бальмеровских) собственных значений.

Квазиклассическое приближение в широком смысле слова (синонимы: высокочастотная асимптотика, коротковолновое приближение, приближение геометрия, оптики, метод ВКБ, метод эйконала) - асимптотика решений дифференциальных уравнений с частными производными с действительными характеристиками вида

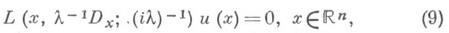
а также систем дифференциальных и псевдодифференциальных уравнений. Здесь 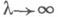- большой параметр, символ L(x, p;e) слабо зависит от e. Уравнению (9) отвечают уравнения классич. механики - уравнение Гамильтона - Якоби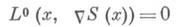

и система Гамильтона

где L⁰=L(x, р;0). К. п. строится с помощью канонич. оператора, отвечающего инвариантным относительно динамич. системы (10) лагранжевым многообразиям, и имеет вид, аналогичный (8).

К. п. широко применяется в современной физике, в задачах о распространении звуковых, упругих, электромагнитных волн, в нерелятивистской и релятивистской квантовой механике и других вопросах.

Лит.:[1] Бриллюэн Л., Атом Бора, пер. с франц., Л.- М., 1935; [2] Ландау Л. Д., Лившиц Е. М., Квантовая механика, 2 изд., М., 1963 (Теоретическая физика, т. 3); [3] Маслов В. П., Теория возмущений и асимптотические методы, М., 1965; [4] Маслов В. П., Федорюк М. В., Квазиклассическое приближение для уравнений квантовой механики, М., 1976; [5] Фок В. А., Проблемы дифракции и распространения электромагнитных волн, М., 1970; [6] Бабич В. М., Булдырев В. С, Асимптотические методы в задачах дифракции коротких волн, М., 1972; [7] Маслов В. П., Операторные методы, М., 1973.

М. В. Федорюк.