КВАЗИИНФОРМАЦИОННОЕ РАСШИРЕНИЕ

бескоалиционной игры - бескоалиционная иградля к-рой заданы отображения и удовлетворяющие при всех условиям: 1) 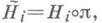2)p_i(s||c_i(s_i))=s_i, где p_i -композиция отображения p и проекции К. р. игры Г может интерпретироваться как результат установления определенной схемы взаимодействия игроков в процессе выбора ими своих стратегий s_i в игре Г. Стратегии s_i соответствуют правилам, определяющим поведение игрока iв любой ситуации, с к-рой он может встретиться. Отображение я сопоставляет набору правил поведения игроков их реализацию, т. е. набор стратегий s_i, к-рые будут выбраны игроками, придерживающимися данных правил. Условие 1) определения К. р. является тогда определением функций выигрыша новой игры Г, а условие 2) выражает сохранение у каждого игрока старых стратегий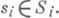

Ситуация s* игры Г тогда и только тогда является образом ситуации равновесия какого-либо К. р.игры Г при соответствующем отображении я, когда для любого и любой найдется такая ситуация что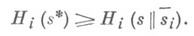

Особенно широко понятие К. р. используется в теории игр с иерархической структурой, где неформальная задача оптимизации информационной схемы трансформируется в задачу построения К. р. заданной игры, дающего первому игроку наилучший результат. Рассматриваются также классы К. р., удовлетворяющих условиям, выражающим те или иные ограничения на информированность игроков. Напр., если Г - игра двух лиц (J={1, 2}), то говорят, что в К. р. игрок 1 не имеет (собственной) информации о стратегии s₂, если для каждой найдется такая что (s₁)S₂. Наилучшим среди К. р., удовлетворяющих этому условию, является, напр., "игра Г ₃", в то время как наилучшим среди всех К. р. является "игра Г ₂".

Лит.:[1] Гермейер Ю. Б., Игры с непротивоположными интересами, М., 1976; [2] Кукушкин Н. С, Морозов В. В., Теория неантагонистических игр, ч. 2, М., 1977.

Н. С. Кукушкин.