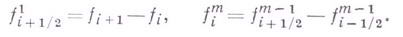ГАУССА ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА
- ГАУССА ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА
формула, использующая в качестве узлов интерполяции ближайшие к точке интерполирования хузлы. Если  то формула
то формула
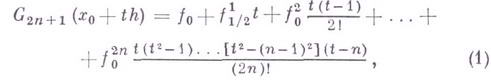
написанная по узлам 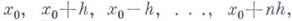
 наз. формулой Гаусса для интерполирования вперед, а формула
наз. формулой Гаусса для интерполирования вперед, а формула
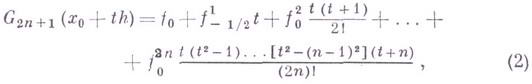
написанная по узлам  наз. формулой Гаусса для интерполирования назад (см. [1], [2]). В формулах (1) и (2) использованы конечные разности, определяемые следующим образом:
наз. формулой Гаусса для интерполирования назад (см. [1], [2]). В формулах (1) и (2) использованы конечные разности, определяемые следующим образом:
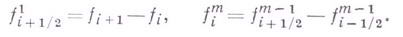
Преимущество Г. и. ф. состоит в том, что указанный выбор узлов интерполяции обеспечивает наилучшую оценку остаточного члена по сравнению с любым другим выбором, а упорядоченность узлов по мере их близости к точке интерполяции уменьшает вычислительную погрешность интерполирования.
Лит.:[1] Березин И. С., Жидков Н. П., Методы вычислений, т. 1, 3 изд., М., 1966; [2] Бахвалов Н. С., Численные методы, М., 1973. М. К. Самарин.
Математическая энциклопедия. — М.: Советская энциклопедия.
И. М. Виноградов.
1977—1985.
Смотреть что такое "ГАУССА ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА" в других словарях:
ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА — формула для приближенного вычисления значений функции f(x), основанного на замене приближаемой функции f(x)более простой в каком то смысле функцией наперед заданного класса, причем параметры ai, i=0, 1, ..., п, выбираются таким образом, чтобы… … Математическая энциклопедия
БЕССЕЛЯ ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА — формула, определяемая как полусумма формулы Гаусса (см. Гаусса интерполяционная формула).для интерполирования вперед по узлам и формулы Гаусса того же порядка для интерполирования назад по отношению к узлу т. е. по совокупности узлов С… … Математическая энциклопедия
Интерполяционная формула Гаусса — формула, использующая в качестве узлов интерполяции ближайшие к точке интерполирования x узлы. Если , то формула написанная по узлам , называется формулой Гаусса для интерполирования вперед, а формула … Википедия
СТИРЛИНГА ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА — полусумма Гаусса интерполяционной формулы для интерполирования вперед по узлам х 0, x0+h, х0 h, . . ., x0+nh, x0 nh в точке x=x0+th и формулы Гаусса того же порядка для интерполирования назад по узлам х 0, х0 h, x0+h , . . ., x0 nh, x0+nh С… … Математическая энциклопедия
ЭВЕРЕТТА ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА — способ записи интерполяционного многочлена, получающегося из Гаусса интерполяционной формулы для интерполирования вперед по узлам x0, x0+h, х 0 h, . . ., x0+nh, x0 nh, x0+(n+1)h в точке x=x0+th исключением конечных разностей нечетного порядка при … Математическая энциклопедия
КВАДРАТУРНАЯ ФОРМУЛА — приближенная формула для вычисления определенного интеграла: в левой части стоит интеграл, подлежащий вычислению. Подинтегральная функция записана в виде произведения двух функций. Первая из них р(х)считается фиксированной для данной К. ф. и наз … Математическая энциклопедия
КУБАТУРНАЯ ФОРМУЛА — формула для приближенного вычисления кратных интегралов вида Интегрирование выполняется по множеству в евклидовом пространстве К. ф. наз. приближенное равенство Подинтегральная функция записана в виде произведения двух функций: первая… … Математическая энциклопедия
Гаусс, Карл Фридрих — У этого термина существуют и другие значения, см. Гаусс. Карл Фридрих Гаусс Carl Friedrich Gauß … Википедия
К. Гаусс — Карл Фридрих Гаусс Carl Friedrich Gauß Дата рождения: 30 апреля 1777 Место рождения: Брауншвейг Дата смерти: 23 февраля 1855 Место смерти … Википедия
Карл Гаусс — Карл Фридрих Гаусс Carl Friedrich Gauß Дата рождения: 30 апреля 1777 Место рождения: Брауншвейг Дата смерти: 23 февраля 1855 Место смерти … Википедия
 то формула
то формула 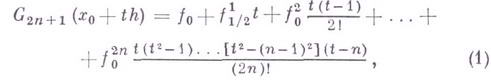
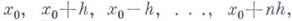
 наз. формулой Гаусса для интерполирования вперед, а формула
наз. формулой Гаусса для интерполирования вперед, а формула 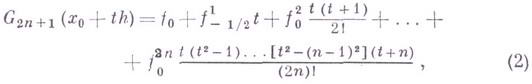
 наз. формулой Гаусса для интерполирования назад (см. [1], [2]). В формулах (1) и (2) использованы конечные разности, определяемые следующим образом:
наз. формулой Гаусса для интерполирования назад (см. [1], [2]). В формулах (1) и (2) использованы конечные разности, определяемые следующим образом: