ИНТЕГРАЛЬНЫЙ ИНВАРИАНТ

степени к(порядка k)гладкой динамической системы - а) абсолютный И. и.: внешняя дифференциальная форма j степени к, переходящая в себя под действием преобразований, образующих эту систему; б) относительный И. и.: внешняя дифференциальная форма j степени k, внешний дифференциал к-рой является абсолютным И. и. (имеющим уже степень k+1).

Обычно речь идет об И. и. для потока {S_t}, определяемого системой обыкновенных дифференциальных уравнений x=f(x), где f - гладкое векторное поле, заданное в нек-рой области евклидова пространства (или многообразия); в терминах координат (локальных координат в случае многообразия) эта система имеет вид

Важный пример И. и.- форма объема (f=p(x)dx₁dx_n [где р(х)- положительная локально интегрируемая (часто даже непрерывная или гладкая) функция координат]. При гладкой р эта форма является абсолютным И. и. системы (1), если В этом случае поток имеет инвариантную меруm(A) = к-рая в терминах (локальных) координат задается своей плотностью р (х)(последнюю, допуская нек-рую вольность речи, тоже часто наз. И. и.).

Гамилътонова система с (обобщенными) импульсами и координатами р _i, q_i, i=1, ..., т, имеет относительный И. и.

и абсолютный И. и.

Этот факт можно положить в основу определения гамильтоновых систем и использовать при развертывании их теории, ибо многие специфич. особенности последней непосредственно связаны с этими И. и. (см.[4], [5]). Внешние степени w^k (в том числе и форма объема w^m) являются абсолютными, а произведения yw^k -относительными И. и. любой гамильтоновой системы, поэтому их наз. универсальными И. и. гамильтоновых систем. С точностью до множителя все универсальные И. и. гамильтоновых систем сводятся к указанным (см. [4], [7]).

Если система (1) имеет абсолютный И. и. j степени к, то для любой k-мерной гладкой цепи с (напр., гладкого k-мерного многообразия)

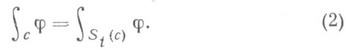
Если же система (1) имеет относительный И. и., то (2), вообще говоря, имеет место лишь тогда, когда цепь является границей цепи размерности k+l. Иногда относительный И. и. определяют несколько более сильным требованием, чтобы (2) выполнялось для всех циклов с. Первоначально И. и. были определены А. Пуанкаре (см. [1], [2]) именно как интегралы указанного выше типа, остающиеся инвариантными, когда область интегрирования движется под действием потока.

Все сказанное легко распространяется на неавтономные системы x=f(x, t). Более существенной является модификация понятия И. и., предложенная Э. Картаном (В. Cartan. [3]) и связанная с переходом (даже в автономном случае) к расширенному фазовому пространству (к обычным фазовым переменным добавляется время), в к-ром интегральные кривые рассматриваемой системы дифференциальных уравнений образуют нек-рое семейство линий (конгруэнцию). Э. Картан требует, чтобы интеграл формы ф по цепи с(или по циклу, если речь идет об относительном И. и.) оставался неизменным, когда каждую точку 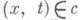сдвигают вдоль интегральной кривой, проходящей через эту точку; при этом различные точки можно сдвигать по-разному, лишь бы это было гладкой деформацией цикла с. (Напр., в новом смысле относительным И. и. гамильтоновой системы является не y, а весьма полезный интегральный инвариант Пуанкаре- Картан а -Hdt, где H- гамильтониан, см. [3]-[5].)

Родственное определение дано в [6].

Лит.:[1] Poincare H., "Acta math.", 1890. t. 13, p. 1-270; [2] Пуанкаре А., Избр. тр., пер. с франц., т. 2, М., 1972; [3] Картан Э., Интегральные инварианты, пер. с франц., М.- Л., 1940; [4] Гантмахер Ф. Р., Лекции по аналитической механике, М., 1960; [5] Арнольд В. И., Математические методы классической механики, М., 1974; [6] Годбийон К., Дифференциальная геометрия и аналитическая механика, пер. с франц., М., 1973; [7] Hwa-Chung Lee, "Proc. Roy. Soc. Edinbourgh", ser. A, 1947, v. 62, p. 237 - 46.

Д. В. Аносов,