- ИЗГИБАНИЕ
- изометрическая деформация подмногообразия Мв римановом пространстве V, т. е. деформация, при к-рой длины кривых на Мне изменяются. Задача об И. поверхностей ведет свое начало от К. Гаусса (С. Gauss) и принадлежит к числу основных проблем дифференциальной геометрии.
Помимо общего случая, было достаточно широко исследовано И. поверхности с сохранением нек-рой внешнегеометрич. характеристики; при этом обычно оказывалось, что лишь поверхности определенного класса допускают такого рода И. Сюда относятся, напр.: 1) поверхности, изгибающиеся с сохранением средней кривизны (поверхности постоянной средней кривизны и, в частности, минимальные поверхности, нек-рые поверхности, наложимые на поверхность вращения); 2) поверхности, изгибающиеся с сохранением одного семейства асимптотич. линий (этот класс составляют линейчатые поверхности);3) поверхности, допускающие изгибание на главном основании, и т. д.
По своему характеру задачу об И. поверхности в евклидовом пространстве условно можно разделить на изгибание в малом, т. е. И. какой-нибудь достаточно малой окрестности UP нек-рой точки Рповерхности, и изгибание в целом, т. е. И. произвольного заранее заданного куска поверхности или полной поверхности. Как правило, любая поверхность допускает И. в малом; однако если Рявляется точкой уплощения, то при нек-рых условиях и при сильных предположениях регулярности допускаемых деформаций Up оказывается неизгибаемой даже в малом.
Первыми утверждениями, касающимися И. в целом, были теорема Э. Либмана (Е. Liebmann) о неизгибаемости сферы, а также результат Д. Гильберта (D. Hilbert): максимум изгиба куска сферы достигается на границе. Дальнейшими исследованиями установлено, что любая замкнутая выпуклая поверхность неизгибаема в классе выпуклых поверхностей без всяких дополнительных условий регулярности. Найдены также теоремы типа принципа максимума, относящиеся к И. произвольного куска выпуклой поверхности класса С 3, из к-рых следует неизгибаемость замкнутой выпуклой поверхности. Однако доказано, что, напр., сфера в классе С 1 допускает изгибания того же класса.
Относительно И. замкнутых поверхностей положительного рода установлены лишь частные результаты; так, напр., поверхности типа Т(тора), т. е. поверхности, состоящие из конечного числа областей с кусочно гладкими границами, в каждой из к-рых гауссова кривизна Кне меняет знака и обращается в нуль только на границе, причем полная кривизна всех областей с К>0 равна 4p,- неизгибаемы при нек-рых дополнительных условиях (аналитичность, отсутствие двух замкнутых асимптотических), в частности, обыкновенный тор неизгибаем.
Полные незамкнутые поверхности, как правило, изгибаемы. Полная выпуклая поверхность Sнеизгибаема, если
 и допускает И., если
и допускает И., если 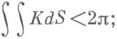 произвол допускаемых ею И. определяется И. ее предельного конуса. Нек-рые классы полных поверхностей отрицательной кривизны также допускают И., таковы, напр., минимальные поверхности, в частности катеноид изгибания в геликоид.
произвол допускаемых ею И. определяется И. ее предельного конуса. Нек-рые классы полных поверхностей отрицательной кривизны также допускают И., таковы, напр., минимальные поверхности, в частности катеноид изгибания в геликоид.Исследования И. незамкнутых поверхностей с границей также относятся главным образом к поверхностям знакопостоянной гауссовой кривизны, причем детально рассмотрен случай, когда И. определяется единственным образом различного рода граничными условиями. Так, напр., при любом И. выпуклой поверхности Fхотя бы одна точка ее края дF изменяет свое расстояние от нек-рой фиксированной точки О, из к-рой Fвидна изнутри и к-рая расположена вне выпуклой оболочки (так что Fнеизгибаема, если расстояние любой точки края дF от Онеизменно); аналогично, при любом И. выпуклой поверхности F, однозначно проектирующейся на плоскость p и ограниченной плоским контуром, хотя бы одна точка края дF изменяет свое расстояние от p (так что Fне допускает изгибаний скольжения- таких П., при к-рых точки края движутся параллельно нек-рой плоскости я); при И. поверхности этого типа хотя бы в одной точке кривизна x края дF меняется, причем число перемен знака разности кривизн краев поверхности Fи ее изгибания F' не менее четырех (так что если кривизна края не изменяется, то Fнеизгибаема). Что касается поверхностей отрицательной кривизны, то достаточно широкий класс их И. получается при решении задачи Коши для уравнений Гаусса и Петерсона - Кодацци, так, напр., И. куска поверхности с K<0, ограниченного отрезками a0, а 1 геодезических и двумя отрезками b0, b1 их ортогональных траекторий однозначно определяется И. края b0. Относительно И. поверхностей знакопеременной кривизны ряд результатов получен лишь для поверхностей вращения.
Для изучения И. поверхностей применяются методы теории уравнений с частным производными, напр., эллиптич. типа, к-рыми описываются И. поверхностей положительной гауссовой кривизны, а также И. поверхностей с сохранением средней кривизны; кроме того, для выпуклых поверхностей особую роль играют методы прямых предельных переходов от многогранников (см. Склеивания метод )в комбинации с теоремами о регулярности поверхности, имеющей регулярную метрику. При достаточной близости выпуклой поверхности F-F0 к ее изгибанию F1 исследование И. сводится с помощью Кон-Фоссена преобразования к аналогичным задачам теории бесконечно малых изгибаний так наз. серединной поверхности
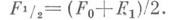
Лит.:[1] Каган В. Ф., Основы теории поверхностей, ч. 2, М.- Л., 1948; [2] Шуликовский В. И., Классическая дифференциальная геометрия, М., 1963; [3] Ефимов Н. В., Качественные вопросы деформаций поверхностей "в малом", "Тр. матем. ин-та АН СССР", 1949 т. 30; [4] его же, "Успехи матем. наук", 1948, т. 3, в. 2, с. 47-158; [5] Погорелов А. В., Изгибание выпуклых поверхностей, М.- Л., 1951; [6] Бляшке В., Дифференциальная геометрия, пер. с нем., т. 1, М.- Л., 1935; [7] Кон-Фоссен С. Э., Некоторые вопросы дифференциальной геометрии в целом, М., 1959.
М. И. Войцеховский.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
