- ДИССИПАТИВНЫЙ ОПЕРАТОР
- линейный оператор Ас областью определения DA, плотной в гильбертовом пространстве Н, и такой, что
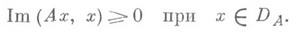
Иногда это требование заменяется условием
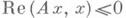при 
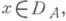т. е. диссипативность Ав этом смысле эквивалентна диссипативности оператора (-iA).Д. о. наз. максимальным, если он не имеет собственных диссипативных расширений. Д. о. всегда допускает замыкание, к-рое также будет Д. о., в частности максимальный Д. о.- замкнутый оператор. Всякий Д. о. допускает расширение до максимального. Для Д. о. все точки Xс Im l<0 есть точки регулярного типа, при этом
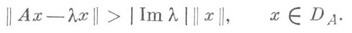
Д. о. является максимальным тогда и только тогда, когда при всех Xс Im l<0 имеет место (А-lI)DA=H. Эквивалентное условие максимальности Д. о. А- его замкнутость и выполнение условия
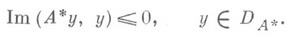
Если А 0- максимальный симметрический оператор, то либо А 0, либо (- А 0 )является максимальным Д. о. Для произвольного симметрич. оператора А 0 можно рассматривать диссипативные и, в частности, максимальные диссипативные расширения; задача их описания эквивалентна задаче описания всех максимальных диссипативных расширений консервативного оператора B0=iA0: Re( В 0 х, х) = 0,
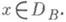
Д. о. тесно связаны со сжатиями и с так наз. аккретивными. операторам и, т. е. такими операторами А, для к-рых iA есть Д. о. В частности, аккретивный оператор Амаксимален тогда и только тогда, когда (-А)является порождающим оператором (генератором) непрерывной однопараметрич. полугруппы сжатийв Н. С помощью преобразований Кэли
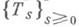
где А- максимальный аккретивный оператор, а Т- сжатие, не имеющее l=1 собственным значением, строится функциональное исчисление и, в частности, теория дробных степеней максимальных Д. о.
Для ограниченных линейных операторов Аопределение Д. о. эквивалентно требованию
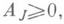где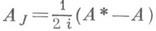 
- мнимая компонента оператора А. Для вполне непрерывного Д. о. в сепарабельном гильбертовом пространстве Нс ядерной мнимой компонентой AJ имеются многочисленные критерии (т. е. необходимые и достаточные условия) полноты системы их корневых векторов. Напр.,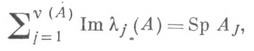
где lj (А)- все собственные значения оператора А, j=1, ...,
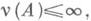a SpAJ -след оператора AJ (критерий Лившица);
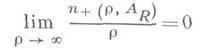или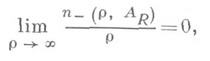 
где
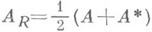- действительная компонента оператора А, а 
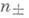- количество характеристич. чисел оператора А R в отрезках [0, r] и [-r, 0] (критерий Крейна). Система {yj} собственных векторов, отвечающих различным собственным числам lj, j=1, 2, ... Д. о., образует базис своей замкнутой линейной оболочки, эквивалентный ортонормированному, если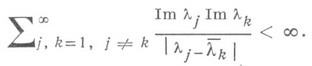
Понятие Д. о. введено и для нелинейных и даже многозначных операторов А. Такой оператор в гильбертовом пространстве наз. Д. о., если для любых двух его значений
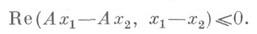выполнено неравенствоЭто понятие лежит в основе теории однопараметрических нелинейных сжимающих полугрупп и связанных с ними дифференциальных уравнений. Другое обобщение понятия Д. о. относится к операторам, действующим в банаховых пространствах с так называемым полувнутренним произведением. Наконец, имеется обобщение, связанное с операторами, действующими в гильбертовом пространстве с индефинитной метрикой.
Лит.:[1] Секефальви-Надь Б., Фояш Ч,, Гармонический анализ операторов в гильбертовом пространстве, пер. с франц., М., 1970; [2] Крейн С. Г., Линейные дифференциальные уравнения в банаховом пространстве, М., 1967; [3] Лившиц М. С, "Матем. сб.", 1954, т. 34, № 1, с. 145- 99; [4] Филлипс Р. С, "Математика", 1962, т. 6, № 4, с. 11 - 70; [5] Crandall M., Рагу A., "J. Funet. Analys.", 1969, v 3, p. 376-418; [6] Lumer G., Phillips R., "Pacific J Math.", 1961, v. 11, p. 679 - 98.
И. С. Иохвидов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
