РАСШИРЕНИЕ

о п е р а т о р а - линейный оператор, график к-рого содержит график данного линейного оператора. Тот факт, что оператор Весть Р. оператора А, записывается в виде АМ В. Обычные задачи теории Р.: максимально расширить оператор, сохраняя определенное свойство, или изучить Р. оператора, обладающие нек-рым дополнительным свойством.

Пусть, напр., дан изометрич. оператор Ав гильбертовом пространство Нс областью определения D(А)МНи областью значений R(A)МH; тогда изометрические Р. оператора Анаходятся во взаимно однозначном соответствии с изометрич. отображениями из в . В 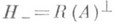частности, Аимеет унитарные Р., когда размерности и 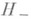совпадают.

Р а с ш и р е н и я с и м м е т р и ч е с к и х о п ер а т о р о в. Наиболее развитой (и важной для приложений) является теория самосопряженных Р. симметрия, операторов в гильбертовом пространстве. Оператор Тявляется симметрическим тогда и только тогда, когда ТМ Т*, где Т*- сопряженный к Топератор. Поэтому область определения любого симметрического Р. оператора Тсодержится в D( Т*), и это Р. есть с у-ж е н и е оператора Т*. Тем самым описание симметрических Р. сводится к нахождению их областей определения. Подпространство LМD( Т* )является областью определения нек-рого симметрического Р. оператора Ттогда и только тогда, когда 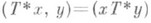для любых . Оказывается, что

где 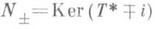- д е ф е к т н ы е п о д п р о с тр а н с т в а (их размерности 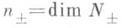наз. д е-ф е к т н ы м и ч и с л а м и), и симметрические Р. оператора Тнаходятся во взаимно однозначном соответствии с изометрич. отображениями из 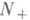в : каждому такому отображению V соответствует Р. оператора Тс областью определения , где Гv - график оператора V. Самосопряженные Р. соответствуют унитарным операторам Vи, следовательно, существуют тогда и только тогда, когда дефектные числа равны. Области определения Р. симметрич. операторов удобно описывать с помощью т. н. (абстрактных) граничных условий. Г р а н и ч н ы м з н а ч е н и е м для симметрич. оператора Тназ. всякий линейный функционал на D( Т*), непрерывный относительно нормы 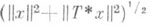и равный нулю на D(Т);г р а н и ч н ы м у с л о в и е м наз. уравнение f(x) = 0, где f - граничное значение. Граничные значения определяются своими значениями на 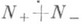. Если дефектные числа симметрич. оператора Т конечны, то всякое его симметрич. расширение 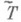определяется семейством граничных условий, то есть , где f_i - граничные значения. Семейства граничных значений, определяющие самосопряженные Р. оператора Тсдефектными числами , описываются следующим образом. Пусть j₁, ... , j_n - ортонормированный базис в , а ^_ и пусть для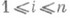

Тогда всякое самосопряженное расширение 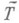оператора Топределяется граничными условиями

где - унитарная 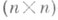-матрица.

В нек-рых случаях удается установить существование самосопряженных Р. (и найти нек-рые из них), не решая трудной задачи нахождения дефектных подпространств и дефектных чисел. Напр., если Т коммутирует с (антиунитарной) инволюцией пространства H, то он допускает самосопряженное Р. Это часто используется в теории дифференциальных операторов, где в качестве инволюции берется комплексное сопряжение пространства . Равенство дефектных чисел имеет место и в том случае, когда на действительной оси есть точки регулярного типа оператора Т (точка l. наз. т о ч к о й р е г у л я р н о г о т и п а, если при нек-ром с>0 и для всех ).

Р а с ш и р е н и я п о л у о г р а н и ч е н н ы х о п е р а т о р о в. Оператор Тназ. п о л у о г р а н и-ч е н н ы м с н и з у числом 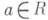, если его ч и с л о в а я о б л а с т ь 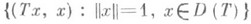лежит в интервале 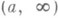; оператор, полуограниченный снизу нулем, наз. п о л о ж и т е л ь н ы м. Если Тполуограничен снизу числом а, то все числа l<а - его точки регулярного типа, дефектные числа равны и существуют самосопряженные Р. Одно из них можно построить следующим образом. Полуторалинейная форма 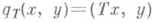, определенная на 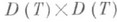, допускает замыкание . Но, как всякой замкнутой симметричной билинейной форме, форме 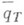соответствует единственный самосопряженный оператор такой, что . Оператор наз. р а с ш и р е н и е м Ф р и д р и х с а оператора Т, он полуограничен, и нижняя грань его спектра равна нижней грани числовой области оператора Т. Это - единственное самосопряженное Р., область определения к-рого содержится в области определения формы . С помощью расширения Фридрихса можно описать другие полуограниченные Р. оператора Т(если дефектные числа оператора Тконечны, то все его самосопряженные Р. полуограничены). Для этого достаточно найти все положительные Р. положительных операторов (общий случай сводится к данному добавлением оператора, кратного единичному). Пусть Т - положительный оператор, , тогда положительные самосопряженные Р. оператора Тоднозначно соответствуют положительным ограниченным операторам Вв L:для каждого такого оператора Вподпространство - область определения соответствующего Р. (см. [4]).

Построение расширения Фридрихса обобщается на с е к т о р и а л ь н ы е о п е р а т о р ы, т. е. операторы, числовая область к-рых содержится в нек-ром угле ; существует Р., являющееся максимальным секториальным оператором, числовая область к-рого находится в том же угле и к-рое обладает свойством минимальности, аналогичным свойству расширения Фридрихса. Рассмотрен случай операторов, действующих из банахова пространства в сопряженное к нему (см. [5]).

Д и с с и п а т и в н ы е р а с ш и р е н и я. В нек-рых задачах возникает необходимость строить симметрические Р. симметрич. операторов. Типичный результат состоит в следующем. Оператор Аназ. д и с с и п а-т и в н ы м, если его числовая область лежит в левой полуплоскости, и м а к с и м а л ь н ы м д и с с и п а-т и в н ы м, если он диссипативен и не имеет диссипативных Р. Всякий симметрич. оператор имеет Р. вида iA, где А - максимальный диссипативный оператор; все такие Р. описываются с помощью сжимающих отображений 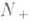в 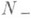(см. [8]).

Р а с ш и р е н и я д и ф ф е р е н ц и а л ь н ы х o n e-р а т о р о в. Важные применения теория Р. операторов имеет при исследовании дифференциальных операторов. Пусть

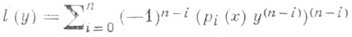
- формально самосопряженное дифференциальное выражение на интервале (a, b); пусть - подпространство, состоящее из всех функций с абсолютно непрерывными квазипроизводными порядков 0, 1, ... , 2 п-1 и 2n-й квазипроизводной, принадлежащей , где D₀ - подпространство в D, состоящее из функции, носители к-рых не содержат концов интервалов. Формула Ту=l (у)при определяет оператор Т;пусть Т'₀ - его сужение на D₀. Оператор T'₀- симметрический, 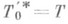и пусть Т ₀=Т'₀ -его замыкание. Область определения оператора Т ₀ в регулярном случае (т. е. когда интервал ( а, b )конечен и функция суммируема) образована всеми функциями из D, первые 2n-1 квазипроизводных к-рых обращаются в 0 на концах интервала. В сингулярном случае D(T₀ )описывается более сложно (см. [2]). Дефектные числа оператора Т ₀ равны, причем в регулярном случае они равны 2n, а в сингулярном - не превосходят 2n. Таким образом, Т ₀ всегда обладает самосопряженными Р.; их спектры, спектральные разложения и резольвенты являются основными объектами теории дифференциальных операторов, поскольку выбор того или иного самосопряженного Р. является фактически точной постановкой нек-рой спектральной задачи. Это особенно наглядно проявляется в регулярном случае: (абстрактные) граничные условия, задающие область определения самосопряженного Р. оператора Т ₀, записывается тогда в виде обычных граничных условий:

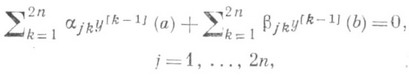
где - набор чисел (такое описание следует из вышеприведенного описания (абстрактных) граничных условий, поскольку в регулярном случае определены

граничные значения

При р ₀ (х)>0оператор Т ₀ является полуограниченным снизу, и его расширение Фридрихса соответствует граничным условиям

В общем случае самосопряженные Р. оператора Т ₀ можно описать следующим образом. Пусть

для любых функций уи z из D;тогда существуют пределы

причем

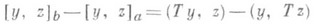
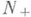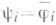(ф о р м у л а Л а г р а н ж а). Поэтому для описания самосопряженных Р. оператора T₀ достаточно выбрать базисы j_l ... , j_n и в дефектных подпространствах и (удобно считать, что ) и каждой унитарной матрице поставить в соответствие самосопряженное расширение T_q, область определения к-рого состоит из всех функций , удовлетворяющих граничным условиям

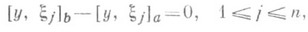
где

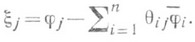
Р а с ш и р е н и я, о т в е ч а ю щ и е к р а е в ы м з а д а ч а м. Р. полуограниченных операторов играют центральную роль в теории эллиптических краевых задач. Пусть, напр., l(у) - эллиптическое дифференциальное выражение 2-го порядка в области G n-мерного пространства и пусть - минимальный и максимальный операторы, определенные этим выражением. Тогда оператор А ₀ положительно определен, его дефектные числа бесконечны и дефектное подпространство L₀=Ker А (оно наз. п р о с т р а н с т в о м l - га р м о н и ч е . с ки х ф у н к ц и й в G) допускает естественную реализацию в виде пространства функций на границе области G. Таким образом, различные Р. оператора А ₀. соответствуют тем или иным граничным условиям и определяют различные краевые задачи. В частности, расширение Фридрихса определено на всех функциях из пространства Соболева , обращающихся в нуль на 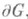, и уравнение 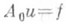соответствует задаче Дирихле:

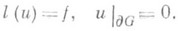
Теория уравнений с частными производными диктует постановку многих общих задач о Р. симметрич. операторов. Среди них задачи об условиях единственности самосопряженного Р. (т. н. с у щ е с т в е н н а я с а м о с о п р я ж е н н о с т ь), о существовании коммутирующих Р. у коммутирующих (в том или ином смысле) симметрич. операторов, о существовании промежуточных Р. с заданными свойствами (напр., с условиями на спектр) и т. д. (см. [7] - [9]).

Р а с ш и р е н и я с в ы х о д о м и з г и л ь б е р т о в а п р о с т р а н с т в а. Всякий симметрич. оператор, действующий в гильбертовом пространстве Н, может быть расширен до самосопряженного оператора, действующего в нек-ром пространстве H₁ ЙH(см. [10]), откуда следует существование у всякого симметрич. оператора обобщенной спектральной функции. С этим также связаны различные результаты о Р. с выходом из пространства и дилатациях (см. [11]). Так, всякое с ж а т и е, т. е. оператор с нормой , гильбертова пространства может быть расширено до коизометрического (т. е. сопряженного к изометрическому) оператора; всякое сжатие, степени к-рого сильно сходятся к нулю, может быть расширено до обратного одностороннего сдвига (т. о. сопряженного к одностороннему сдвигу). Результаты о Р. с выходом из пространства обобщаются на коммутативные семейства, полугруппы и т. д.

Лит.:[1] Д а н ф о р д Н., Ш в а р ц Д ж.- Т., Линейные операторы, пер. с англ., т. 2, М., 1966; [2] Н а й м а р к М. А., Линейные дифференциальные операторы, 2 изд., М., 1969; [3] К а т о Т., Теория возмущения линейных операторов, пер. с англ., М., 1972; [4] К р е й н М. Г.,"Матем. сб."., 1947, т. 20, с. 431-98, т. 21, с. 365-404; [5] Б и р м а н М. Ш., там же, 1956, т. 38, с. 431-50; [6] Ф и л л и п с Р. С., "Математика", 1962, т. 6, № 4, с. 11-70; [7] М о р е н К., Методы гильбертова пространства, пер. с польск., М., 1965; [8] Б е р е з а н с к и й Ю. М., Разложение по собственным функциям самосопряженных операторов, К., 1965; [9] М и х л и н С. Г., Проблема минимума квадратичного функционала, М.- Л., 1952; [10] Н а й м а р к М. А .,"Изв. АН СССР. Сер. матем.", 1940, т. 4, с. 277-318; [11] С е к е ф а л ь в и - Н а д ь Б., Ф о я ш Ч., Гармонический анализ операторов в гильбертовом пространстве, пер. с франц., М., 1970; [12] В r о w n L., D о u g I a s R., F i l-l m о r е Р., в кн.: Ргос. Conference operator theory, В.- [а. <о.], 1973; [13] А г v е s о n W., "Duke math. J.", 1977, v. 44, № 2, p. 329-55; [14] Р и д М., С а й м о н Б., Методы современной математической физики, пер. с англ., т. 2 - Гармонический анализ. Самосопряженность, М., 1978.,

А. II. Логинов, В. С. Шулъман.