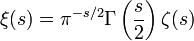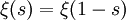Римана дзета-функция

Дзета-функция Римана ζ(s) определяется с помощью ряда Дирихле:

$\zeta(s) = \frac{1}{1^s}+\frac{1}{2^s}+\frac{1}{3^s}+\ldots$.

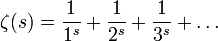В области 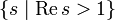$\left\{ s\mid\operatorname{Re}\,s > 1\right\}$, этот ряд сходится, является аналитической функцией и допускает аналитическое продолжение на всю комплексную плоскость без единицы. В этой области также верно представление в виде бесконечного произведения (тождество Эйлера)

$\zeta(s) = \prod_p \frac{1}{1 - p^{-s}}$ ,

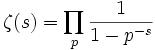где произведение берётся по всем простым числам p. Это равенство представляет собой одно из основных свойств дзета-функции.

Свойства

• Существуют явные формулы для значений дзета-функции в чётных целых точках:

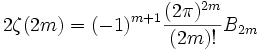  $2\zeta(2m) = (-1)^{m+1} \frac{(2\pi)^{2m}}{(2m)!} B_{2m}$, где B_2m — число Бернулли.

  • В частности, $\zeta(2) = \frac{\pi^2}{6}$, $\zeta(4) = \frac{\pi^4}{90}$.
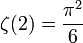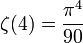• Про значения дзета-функции в нечётных целых точках известно мало: предполагается, что они являются иррациональными и даже трансцендентными, но пока доказана только лишь иррациональность числа ζ(3) (Роже Апери, 1978). Есть также результаты, показывающие, что среди некоторого множества значений дзета-функции в следующих нечетных точках есть хотя бы одно иррациональное.
• При $\operatorname{Re}\,s> 1$
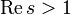
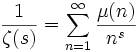  • $\frac1{\zeta(s)}=\sum_{n=1}^\infty\frac{\mu(n)}{n^s}$, где μ(n) — функция Мёбиуса
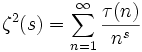  • $\zeta^2(s)=\sum_{n=1}^\infty\frac{\tau(n)}{n^s}$, где τ(n) — число делителей числа n
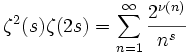  • ${\zeta^2(s)}{\zeta(2s)}=\sum_{n=1}^\infty\frac{2^{\nu(n)}}{n^s}$, где ν(n) — число простых делителей числа n
• ζ(s) имеет в точке s = 1, простой полюс с вычетом, равным 1.
• Дзета-функция при 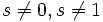$s\ne 0, s\ne 1$ удовлетворяет уравнению:

  $\zeta(s) = 2^s \pi^{s-1} \sin{\pi s \over 2} \Gamma(1-s) \zeta(1-s)$,

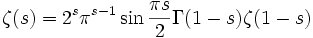где Γ(z) — Гамма-функция Эйлера. Это уравнение называется функциональным уравнением Римана.

• Для функции

  $\xi(s)=\pi^{-s/2}\Gamma\left(\frac{s}{2}\right)\zeta(s)$

введенной Риманом для исследования ζ(s) и называемой кси-функцией Римана, это уравнение принимает вид

$\ \xi(s)=\xi(1-s)$

Нули дзета-функции

Основная статья: Гипотеза Римана

Как следует из функционального уравнения Римана, в полуплоскости 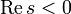$\operatorname{Re}\,s< 0$, функция ζ(s) имеет лишь простые нули в отрицательных чётных точках: 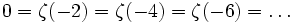$0 = \zeta(-2) = \zeta(-4) = \zeta(-6) = \dots$. Эти нули называются «тривиальными» нулями дзета-функции. Далее 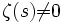$\zeta(s)\not=0$ при вещественных 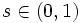$s\in (0,1)$. Таким образом, все «нетривиальные» нули дзета-функции являются комплексными числами, обладают свойством симметрии относительно вещественной оси и относительно вертикали 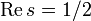$\operatorname{Re}\,s=1/2$ и лежат в полосе 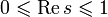$0\leqslant\operatorname{Re}\,s\leqslant 1$, которая называется критической полосой. Гипотеза Римана состоит в том, что все «нетривиальные» нули дзета-функции находятся на прямой 1 / 2 + it.

История

Как функция вещественной переменной, дзета-функция была введена в 1737 году Эйлером, который и указал её разложение в произведение. Затем эта функция рассматривалась Дирихле и, особенно успешно, Чебышёвым при изучении закона распределения простых чисел. Однако наиболее глубокие свойства дзета-функции были обнаружены позднее, после работы Римана (1859), где дзета-функция рассматривалась как функция комплексной переменной.

Ссылки

• Jonathan Sondow and Eric W. Weisstein Riemann Zeta Function на сайте Wolfram MathWorld.(англ.)