ДАНИЕЛЯ ИНТЕГРАЛ

- расширение понятия интеграла, предложенное П. Даниелем [1]. Схема построения этого интеграла наз. схемой Даниеля, представляет собой продолжение на более широкий класс функций интеграла, определенного первоначально для нек-рой совокупности функций, называемых элементарными функциями. При сохранении способа продолжения изменение объема исходной совокупности элементарных функций приводит к разным расширениям понятия интеграла. В этой схеме аксиоматизируется понятие элементарного интеграла, в отличие от схемы Лебега (см. Лебега интеграл), аксиоматизирующей понятие меры.

Пусть X- произвольное множество и L₀- некоторая совокупность определенных на Xдействительных ограниченных функций; эти функции наз. элементарными. Предполагается, что L₀- векторная решетка, т. <е. из f,и

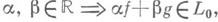
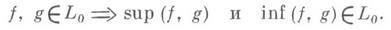
Пусть на L₀ определен функционал I(f), принимающий действительные значения и такой, что

если 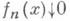для любого х, то 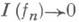(непрерывность относительно монотонной сходимости).

Такой функционал наз. интегралом от элементарных функций, или элементарным интегралом. Множество наз. множеством меры нуль, если для любого e>0 найдется такая неубывающая последовательность что sup 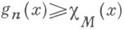, где c_M (х)- характеристич. функция множества М:

Функция f(x), определенная на X, принадлежит классу L⁺, если существует такая последовательность что почти всюду и . Число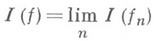

наз. интегралом от f. Интеграл I(f) не зависит от выбора аппроксимирующей последовательности {f_n}. Классом Lназ. совокупность функций f, определенных на Xи представимых в виде f=f₁-f₂, где 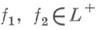. Функции класса Lназ. суммируемыми, а число

- интегралом Даниеля от функции f.

Класс Lс точностью до множества меры нуль является векторной решеткой конечных функций, замкнутой относительно сходимости почти всюду с ограниченными интегралами, и Д. и. от суммируемых функций обладает свойствами дистрибутивности, неотрицательности, непрерывности (относительно сходимости почти всюду), мажорированной суммируемой функцией (теорема Лебега о переходе к пределу под знаком интеграла), а также рядом других естественных свойств интеграла.

В том случае, когда Х=[ а, b]и L₀ есть совокупность ступенчатых функций

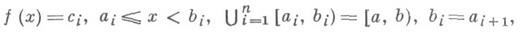
Д. и. совпадает с интегралом Лебега от функций, суммируемых на [ а, b]. Схема Даниеля применима для построения интеграла от функций со значениями в s-полной решетке.

Лит.:[1] Daniеll P., "Ann. Math.", 1917, v. 19, p. 279 -94; [2] Шилов Г. Е., Гуревич Б. Л., Интеграл, мера и производная, 2 изд., М., 1967; [3] Люмис Л., Введение в абстрактный гармонический анализ, пер. с англ., М., 1956.

В. И. Соболев.