гессиан — сущ., кол во синонимов: 1 • определитель (10) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
Гессиан — Функциональным определителем n функций: f1, f2, f3,.. . fn от n независимых переменных x1, x2, x3 ... xn называется определитель вида: df1/dx1, df1/dx2,.. . df1/dxn df2/dx1, df2/dx2,.. . df2/dxn … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
ГЕССИАН — гессиана, алгебраической кривой порядка п множество точек, конические поляры к рых распадаются на две прямые, а также множество двойных точек первых поляр. Г. неособой кривой порядка песть кривая порядка 3(n 2) и класса Если есть уравнение кривой … Математическая энциклопедия
Гессиан функции — Гессиан функции симметрическая квадратичная форма[источник?], описывающая поведение функции во втором порядке. Для функции , дважды дифференцируемой в точке или где … Википедия
Гессиан — … Википедия
Матрица Гессе — Гессиан функции симметрическая квадратичная форма описывающая поведение функции во втором порядке. Для функции f дважды дифференцируемой в точке или где (или … Википедия
Определитель Гессе — Гессиан функции симметрическая квадратичная форма описывающая поведение функции во втором порядке. Для функции f дважды дифференцируемой в точке или где (или … Википедия
Гессе — Не следует путать этот термин с терминами Гесс и Гессен. Гессе (Хессе; нем. Hesse) немецкая фамилия. Образована от названия древнегерманского племени гессы. Известные носители Гессе, Герман (1877 1962) немецко швейцарский писатель … Википедия
Метод одной касательной — Метод Ньютона (также известный как метод касательных) это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643 1727), под именем… … Википедия
Метод Ньютона — Метод Ньютона, алгоритм Ньютона (также известный как метод касательных) это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном… … Википедия
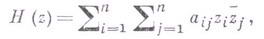
(или 
) и 
задана на n-мерном действительном пространстве 
(или комплексном пространстве 
) с координатами 
(или 
). Введен О. Гессе (О. Hesse, 1844). С помощью локальной системы координат это определение переносится на функции, определенные на действительном многообразии класса 
(или на комплексном пространство). В обоих случаях Г.- квадратичная форма, заданная на касательном пространстве, не зависящая от выбора системы координат. В теории Морса через Г. определяются понятия (не) вырожденной критич. точки, формы Морса и формы Ботта. В комплексном анализе Г. участвует в определении псевдовыпуклой области и плюрисубгармонич. функции.