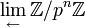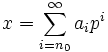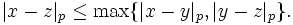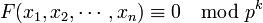- P-адическое число
-
p-адическое число
p-ади́ческое число (произносится: пэ-адическое) — элемент расширения поля рациональных чисел, являющегося пополнением поля рациональных чисел относительно p-адической нормы, которая определяется на основе свойств делимости целых чисел на заданное простое число р.
p-адические числа были введены Гензелем (нем.) в 1897 году[1].
Поле p-адических чисел обычно обозначается
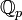 или
или 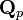 .
.Содержание
Алгебраическое построение
Целые p-адические числа
Стандартное определение
Целым p-адическим числом для произвольного простого p называется бесконечная последовательность
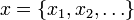 вычетов xn по модулю pn, удовлетворяющих условию
вычетов xn по модулю pn, удовлетворяющих условию 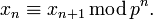
Сложение и умножение целых p-адических чисел определяется как почленное сложение и умножение таких последовательностей. Для них непосредственно проверяются все аксиомы кольца.
Определение через проективный предел
В терминах проективных пределов кольцо целых p-адических чисел определяется как предел
колец
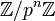 вычетов по модулю pn относительно естественных проекций
вычетов по модулю pn относительно естественных проекций 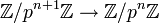 .
.Эти рассмотрения можно провести в случае не только простого числа p, но и любого составного числа m — получится т. н. кольцо m-адических чисел, но это кольцо в отличие от
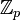 обладает делителями нуля, поэтому дальнейшие построения, рассматриваемые ниже, к нему неприменимы.
обладает делителями нуля, поэтому дальнейшие построения, рассматриваемые ниже, к нему неприменимы.Свойства
Обычные целые числа вкладываются в кольцо p-адических чисел очевидным образом: x = {x,x,...} и являются подкольцом.
Беря в качестве элемента класса вычетов число
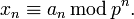 , такое, что
, такое, что 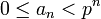 , мы можем записать каждое целое p- адическое число в виде x = {a1,a2,...} однозначным образом. Такой вид называется каноническим. Записывая каждое an в p-ичной системе счисления
, мы можем записать каждое целое p- адическое число в виде x = {a1,a2,...} однозначным образом. Такой вид называется каноническим. Записывая каждое an в p-ичной системе счисления 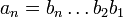 и учитывая что
и учитывая что 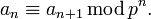 мы можем всякое p-адическое число в каноническом виде представить в виде
мы можем всякое p-адическое число в каноническом виде представить в виде 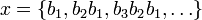 или записывая в виде бесконечной последовательности цифр в p-ичной системе счисления
или записывая в виде бесконечной последовательности цифр в p-ичной системе счисления 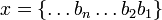 . Действия над такими последовательностями производятся по обыкновенными правилами сложения, вычитания и умножения «столбиком» в p-ичной системе счисления (в нашем примере p=5).
. Действия над такими последовательностями производятся по обыкновенными правилами сложения, вычитания и умножения «столбиком» в p-ичной системе счисления (в нашем примере p=5).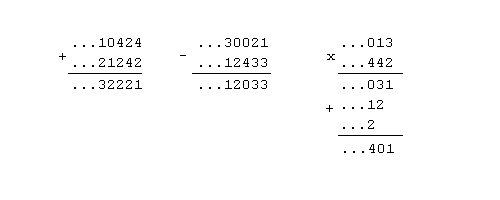
В такой форме записи натуральным числам и нулю соответствуют p-адические числа с конечным числом ненулевых цифр, точно таких, как у исходного числа. Отрицательным числам соответствуют p-адические числа с бесконечным числом ненулевых цифр, например в пятеричной системе −1=…4444=(4).
Кольцо целых p-адических чисел обычно обозначается
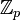 .
.p-адические числа
Определение как поля частных
p-адическим числом называется элемент поля частных
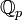 кольца
кольца 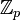 целых p-адических чисел. Это поле называется полем p-адических чисел.
целых p-адических чисел. Это поле называется полем p-адических чисел.Свойства
Поле p-адических чисел содержит в себе поле рациональных чисел. Нетрудно доказать, что любое целое p-адическое число, не кратное p обратимо в кольце
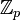 , а кратное p однозначно записывается в виде xpn, где x не кратно p и поэтому обратимо, а n > 0, то ясно, что любой ненулевой элемент поля
, а кратное p однозначно записывается в виде xpn, где x не кратно p и поэтому обратимо, а n > 0, то ясно, что любой ненулевой элемент поля 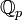 может быть записан в виде xpn, где x не кратно p а n любое, если n отрицательно, то исходя из представления целых p-адических чисел в виде последовательности цифр в p-ичной системе счисления мы можем записать любое такое p-адическое число в виде последовательности
может быть записан в виде xpn, где x не кратно p а n любое, если n отрицательно, то исходя из представления целых p-адических чисел в виде последовательности цифр в p-ичной системе счисления мы можем записать любое такое p-адическое число в виде последовательности 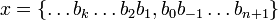 , то есть формально в виде в виде p-ичной дроби с конечным числом цифр после запятой и, возможно, бесконечным числом ненулевых цифр до запятой. Деление таких чисел можно также производить аналогично «школьному» правилу, но начиная с младших, а не старших разрядов числа. Так, в той же пятеричной системе имеем:
, то есть формально в виде в виде p-ичной дроби с конечным числом цифр после запятой и, возможно, бесконечным числом ненулевых цифр до запятой. Деление таких чисел можно также производить аналогично «школьному» правилу, но начиная с младших, а не старших разрядов числа. Так, в той же пятеричной системе имеем: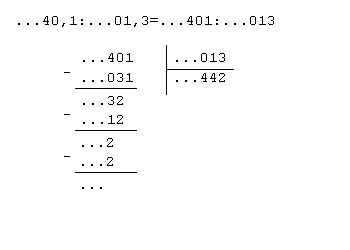
Метрическое построение
Любое рациональное число r можно представить как
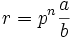 где a и b целые числа, не делящиеся на p, а n — целое. Тогда | r | p — p-адическая норма r — определяется как p − n. Если r = 0, то | r | p = 0.
где a и b целые числа, не делящиеся на p, а n — целое. Тогда | r | p — p-адическая норма r — определяется как p − n. Если r = 0, то | r | p = 0.Поле p-адических чисел есть пополнение поля рациональных чисел с метрикой dp, определённой p-адической нормой: dp(x,y) = | x − y | p. Это построение аналогично построению поля вещественных чисел как пополнения поля рациональных чисел при помощи нормы, являющейся обычной абсолютной величиной.
Норма | r | p продолжается по непрерывности до нормы на
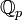 .
.Свойства
- Каждый элемент x-поля p-адических чисел может быть представлен в виде сходящегося ряда
-
- где n0 — некоторое целое число, а ai — целые неотрицательные числа, не превосходящие p − 1, а именно взяв в качестве ai цифры из записи p-адического числа x в виде последовательности цифр в системе счисления с основанием p. Такая сумма всегда сходится в метрике dp к самому x.
- p-адическая норма | x | p удовлетворяет сильному неравенству треугольника
-
- Числа
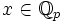 с условием
с условием 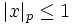 образуют кольцо
образуют кольцо 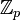 целых p-адических чисел, являющееся пополнением кольца целых чисел
целых p-адических чисел, являющееся пополнением кольца целых чисел 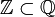 в норме | x | p.
в норме | x | p. - Числа
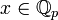 с условием | x | p = 1 образуют мультипликативную группу и называются p-адическими единицами.
с условием | x | p = 1 образуют мультипликативную группу и называются p-адическими единицами. - Совокупность чисел
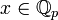 с условием | x | p < 1 является главным идеалом в
с условием | x | p < 1 является главным идеалом в 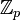 с образующим элементом p.
с образующим элементом p.
- метрическое пространство
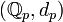 гомеоморфно Канторову множеству, а пространство
гомеоморфно Канторову множеству, а пространство 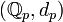 гомеоморфно Канторову множеству с вырезанной точкой.
гомеоморфно Канторову множеству с вырезанной точкой. - Для различных p нормы | x | p независимы, а поля
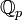 неизоморфны.
неизоморфны. - Для любых элементов
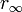 , r2, r3, r5, r7, …, таких что
, r2, r3, r5, r7, …, таких что 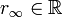 и
и 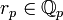 , можно найти последовательность рациональных чисел xn, таких что для любого p,
, можно найти последовательность рациональных чисел xn, таких что для любого p, 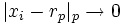 и
и 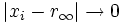 .
.
Применения
- Если
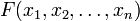 — многочлен с целыми коэффициентами, то разрешимость при всех k сравнения
— многочлен с целыми коэффициентами, то разрешимость при всех k сравнения
-
- эквивалентна разрешимости уравнения
- в целых p-адических числах. Необходимым условием разрешимости этого уравнения в целых или рациональных числах является его разрешимость в кольцах или, соответственно, полях p-адических чисел при всех p, а также в поле вещественных чисел. Для некоторых классов многочленов (например, для квадратичных форм) это условие является также достаточным.
- На практике для проверки разрешимости уравнения в целых p-адических числах достаточно проверить разрешимость указанного сравнения для определенного конечного числа значений k. Например, согласно лемме Гензеля (Hensel’s lemma), при n = 1 достаточным условием для разрешимости сравнения при всех натуральных k служит наличие простого решения у сравнения по модулю p (то есть простого корня у соответствующего уравнения в поле вычетов по модулю p). Иначе говоря, при n = 1 для проверки наличия корня у уравнения в целых p-адических числах, как правило, достаточно решить соответствующее сравнение при k = 1.
Литература
- Боревич З. И., Шафаревич И. Р. Теория чисел, — М.: Наука, 1985.
- Коблиц Н. р-адические числа, р-адический анализ и дзета-функции, — М.: Мир, 1982.
- Серр Ж.-П. Курс арифметики, — М.: Мир, 1972.
- Б. Беккер, С. Востоков, Ю. Ионин 2-адические числа // Квант. — 1979. — Т. 2. — С. 26—31.
- p-адические числа для «чайников»
Ссылки
- ↑ Kurt Hensel Über eine neue Begründung der Theorie der algebraischen Zahlen // Jahresbericht der Deutschen Mathematiker-Vereinigung. — 1897. — Т. 6. — № 3. — С. 83—88.(нем.)
Числа Простые натуральные | целые | рациональные | иррациональные | вещественные | p-адические | алгебраические | трансцендентные Составные комплексные | дуальные | двойные | кватернионы | числа Кэли (октавы) | седенионы | гиперкомплексные
Wikimedia Foundation. 2010.
p-адическое число — Для заданного фиксированного простого числа p p адическое число (произносится: пэ адическое; соответственно: два адическое, три адическое и т.п.) элемент расширения поля рациональных чисел, являющегося пополнением поля рациональных чисел… … Википедия
p-АДИЧЕСКОЕ ЧИСЛО — элемент расширения поля рациональных чисел, получаемого на основе свойств делимости целых чисел на заданное простое число р. Это расширение есть пополнение поля рациональных чисел относительно неархимедова нормирования (см. Абсолютное значение).… … Математическая энциклопедия
Число — У этого термина существуют и другие значения, см. Число (значения). Число основное понятие математики[1], используемое для количественной характеристики, сравнения и нумерации объектов. Возникнув ещё в первобытном обществе из потребностей… … Википедия
Число (матем.) — см. также: Число (лингвистика) Число абстракция, используемая для количественной характеристики объектов. Возникнув ещё в первобытном обществе из потребностей счёта, понятие числа изменялось и обогащалось и превратилось в важнейшее математическое … Википедия
ДИОФАНТОВЫ ПРИБЛИЖЕНИЯ — раздел теории чисел, в к ром изучаются приближения нуля значениями функций от конечного числа целочисленных аргументов. Первоначальные задачи Д. п. касались рациональных приближений к действительным числам, но развитие теории привело к задачам, в … Математическая энциклопедия
ИДЕЛЬ — обратимый элемент кольца аделей. Совокупность всех И. образует по умножению группу, наз. группой иделей. Элементами группы И. поля рациональных чисел являются последовательности вида где ненулевое действительное число, а р отличное от нуля р… … Математическая энциклопедия
Аксиома Архимеда — для отрезков … Википедия
Список известных уроженцев Кёнигсберга — Западный фасад Кёнигсбергского замка на открытке начала XX века Замок Кёнигсберг был основан Тевтонским орденом в 1255 году, вокруг него образовались три города: Альтштадт, Лёбенихт и Кнайпхоф, которые в 1724 году объединились в единый город… … Википедия
АБСОЛЮТНОЕ ЗНАЧЕНИЕ — на теле отображение тела Кв множество действительных чисел, удовлетворяющее условиям: А. з. часто обозначается вместо . А. з. наз. также нормой, мультипликативным нормированием. А. з. могут рассматриваться на любом кольце со значениями в линейно… … Математическая энциклопедия
ОРТОГОНАЛЬНАЯ ГРУППА — группа всех линейных преобразований n мерного векторного пространства Vнад полем k, сохраняющих фиксированную невырожденную квадратичную форму Q на V(т. е. таких линейных преобразований j, что Q(jn(v))=Q(v) для любого ). О. г. принадлежит к числу … Математическая энциклопедия