- ДИОФАНТОВЫ ПРИБЛИЖЕНИЯ
- раздел теории чисел, в к-ром изучаются приближения нуля значениями функций от конечного числа целочисленных аргументов. Первоначальные задачи Д. п. касались рациональных приближений к действительным числам, но развитие теории привело к задачам, в к-рых некоторым действительным функциям необходимо придать "малые" значения при целочисленных значениях аргументов. В силу этого Д. п. тесно связаны с решением неравенств в целых числах - диофантовых неравенств, а также с решением уравнений в целых числах (см. Диофантовы уравнения).
Если рассматриваемая (аппроксимирующая) функция
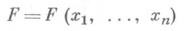 линейна относительно целочисленных аргументов х 1, . .., х п, то Д. п. с функцией Fназ. линейным и, в противном случае - нелинейными. Если F- однородный многочлен от х 1, ..., х п, то Д. п. с функцией Fназ. однородными, а если F- неоднородный многочлен, то - не однородными. Иногда рассматривается одновременно несколько функций F, имеющих хотя бы один общий целочисленный аргумент. В этом случае Д. п. наз. совместными. Совместные Д. п. могут быть линейными или нелинейными, однородными или неоднородными в указанном выше смысле.
линейна относительно целочисленных аргументов х 1, . .., х п, то Д. п. с функцией Fназ. линейным и, в противном случае - нелинейными. Если F- однородный многочлен от х 1, ..., х п, то Д. п. с функцией Fназ. однородными, а если F- неоднородный многочлен, то - не однородными. Иногда рассматривается одновременно несколько функций F, имеющих хотя бы один общий целочисленный аргумент. В этом случае Д. п. наз. совместными. Совместные Д. п. могут быть линейными или нелинейными, однородными или неоднородными в указанном выше смысле.Численные значения Fмогут считаться близкими к нулю не обязательно при

с некоторым е>0, но и при

(односторонние приближения). Функции Fмогут зависеть от параметров, непрерывно меняющихся в некоторой области,- это параметрич. Д. п. Наконец, область определения и область значений аппроксимирующих функций могут быть не только подмножествами евклидова пространства, а существенно иных топологич. пространств (см. ниже Д. п. в поле р-адических чисел и Д. п. в поле степенных рядов).
Наиболее старая ("простейшая") задача Д. п. - приближения нуля линейной формой aх- у, где a>0 - фиксированное действительное число, х, у- переменные целые (линейные однородные Д. п.), т. е. задача о рациональных приближениях к а. Для специальных
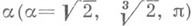 эта задача рассматривалась еще в древности (Архимед, Диофант, Евклид), а ее тесная связь с теорией цепных дробей была вполне выяснена Л. Эйлером (L. Euler) и Ж. Лагранжем (J. Lagrange). В частности, если х 1>0, y1 >0 таковы, что
эта задача рассматривалась еще в древности (Архимед, Диофант, Евклид), а ее тесная связь с теорией цепных дробей была вполне выяснена Л. Эйлером (L. Euler) и Ж. Лагранжем (J. Lagrange). В частности, если х 1>0, y1 >0 таковы, что
где минимум берется по всем целым хв к.-л. интервале
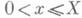 и по всем целым у, то дробь у 1/х 1 является подходящей дробью разложения aв цепную дробь. Если неполные частные разложения ав цепную дробь ограничены, то существует С=С (а)>0 с условием
и по всем целым у, то дробь у 1/х 1 является подходящей дробью разложения aв цепную дробь. Если неполные частные разложения ав цепную дробь ограничены, то существует С=С (а)>0 с условием 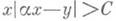 для всех целых x>0, y>0. Это верно, напр., для квадратичных иррациональностей a, так как тогда разложение в цепную дробь периодично. С другой стороны, при любом иррациональном а неравенство
для всех целых x>0, y>0. Это верно, напр., для квадратичных иррациональностей a, так как тогда разложение в цепную дробь периодично. С другой стороны, при любом иррациональном а неравенство 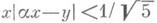 имеет бесконечное число целых решений x>0, y>0, а если
имеет бесконечное число целых решений x>0, y>0, а если 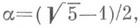 то постоянную
то постоянную 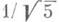 нельзя заменить меньшим числом. Исследование А. А. Маркова о минимумах неопределенных бинарных квадратичных форм позволило продолжить последнее утверждение: если а не эквивалентно (в смысле теории цепных дробей) (
нельзя заменить меньшим числом. Исследование А. А. Маркова о минимумах неопределенных бинарных квадратичных форм позволило продолжить последнее утверждение: если а не эквивалентно (в смысле теории цепных дробей) (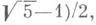 то неравенство х|aх- у|<2-3/2 имеет бесконечное число решений; постоянная 2-3/2 не может быть улучшена, если а эквивалентно
то неравенство х|aх- у|<2-3/2 имеет бесконечное число решений; постоянная 2-3/2 не может быть улучшена, если а эквивалентно  если а не эквивалентно ни (
если а не эквивалентно ни (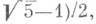 ни
ни  то неравенство х|aх- у|<5 (221)-1/2 имеет бесконечное число решений, и т. д. (см. [1]). Постоянные 5-1/2, 2-3/2,5(221)-1/2, ... монотонно убывают и имеют предел 1/3. Приближения нуля линейным неоднородным многочленом ax+y+b (a, b - действительные числа, х, у- неременные целые) - простейший пример линейных неоднородных диофантовых приближений. П. Л. Чебышев доказал, что при любом иррациональном а и любом b неравенство x|ax+y+b|<2 имеет бесконечное число решений в целых x>0, у. Постоянная 2 здесь не является наилучшей: Г. Минковский (Н. Miukowski) доказал, что если
то неравенство х|aх- у|<5 (221)-1/2 имеет бесконечное число решений, и т. д. (см. [1]). Постоянные 5-1/2, 2-3/2,5(221)-1/2, ... монотонно убывают и имеют предел 1/3. Приближения нуля линейным неоднородным многочленом ax+y+b (a, b - действительные числа, х, у- неременные целые) - простейший пример линейных неоднородных диофантовых приближений. П. Л. Чебышев доказал, что при любом иррациональном а и любом b неравенство x|ax+y+b|<2 имеет бесконечное число решений в целых x>0, у. Постоянная 2 здесь не является наилучшей: Г. Минковский (Н. Miukowski) доказал, что если  ( а, b- целые), то 2 можно заменить на 1/4, что является наилучшей постоянной. Это утверждение есть следствие доказанного самим Г. Минковским простейшего случая гипотезы о произведении неоднородных линейных форм (см. Минковского гипотеза).
( а, b- целые), то 2 можно заменить на 1/4, что является наилучшей постоянной. Это утверждение есть следствие доказанного самим Г. Минковским простейшего случая гипотезы о произведении неоднородных линейных форм (см. Минковского гипотеза).Более сложные задачи общей теории Д. п. касаются аппроксимирующих функций от большего числа целочисленных аргументов (см. Дирихле теорема, Минковского теорема, Кронекера теорема). Удобно ввести функцию
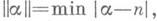 где минимум берется по всем целым п(расстояние от aдо ближайшего целого). Напр., вместо рассмотренных выше линейных многочленов
где минимум берется по всем целым п(расстояние от aдо ближайшего целого). Напр., вместо рассмотренных выше линейных многочленов  и
и 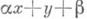 можно брать
можно брать 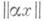 и
и 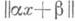 для целых x>0. Из теоремы Дирихле следует, что для любых действительных a1,..., an существует бесконечное число решений системы неравенств
для целых x>0. Из теоремы Дирихле следует, что для любых действительных a1,..., an существует бесконечное число решений системы неравенств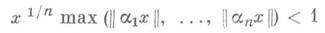
в целых х>0. Единицу можно заменить меньшим числом (напр., n/(n+1)), но ни для какого
 наилучшая постоянная неизвестна. Она не может быть сколь угодно малым числом, как показывает пример 1, a1, . .., an, являющийся базисом действительного алгебраич. поля (см. [1]). Если 1, a1, ..., a п линейно независимы над полем рациональных чисел, то при любых b1, . . ., bn и любом e>0 существует бесконечное число решений системы неравенств
наилучшая постоянная неизвестна. Она не может быть сколь угодно малым числом, как показывает пример 1, a1, . .., an, являющийся базисом действительного алгебраич. поля (см. [1]). Если 1, a1, ..., a п линейно независимы над полем рациональных чисел, то при любых b1, . . ., bn и любом e>0 существует бесконечное число решений системы неравенств
в целых x>0 (теорема Кронекера). Существенная особенность этой теоремы о совместных неоднородных Д. п. состоит в том, что в принципе невозможно (без специальной информации об однородных приближениях к a1, . .., a п). указать скорость убывания e при возрастании х:для того чтобы линейные формы
 "хорошо" аппроксимировали любые числа b1, . . ., bn, необходимо и достаточно, чтобы эти формы не могли "хорошо" аппроксимировать специальный набор чисел b1=0, . . ., bn=0. Различные на первый взгляд задачи Д. п. иногда оказываются тесно связанными. Напр., принцип переноса Хинчина (см. [1]) связывает разрешимость неравенства
"хорошо" аппроксимировали любые числа b1, . . ., bn, необходимо и достаточно, чтобы эти формы не могли "хорошо" аппроксимировать специальный набор чисел b1=0, . . ., bn=0. Различные на первый взгляд задачи Д. п. иногда оказываются тесно связанными. Напр., принцип переноса Хинчина (см. [1]) связывает разрешимость неравенства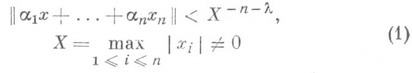
в целых
 числах x1, ..., х п с разрешимостью системы в целых x>0, и обратно: если l1. и m1 соответственно точные верхние грани тех l>0 и m>0, для к-рых (1) и (2) имеют бесконечное число решений, то
числах x1, ..., х п с разрешимостью системы в целых x>0, и обратно: если l1. и m1 соответственно точные верхние грани тех l>0 и m>0, для к-рых (1) и (2) имеют бесконечное число решений, то
В частности, равенства l1=0 n m1=0 равносильны (тогда a1, ...,an соответствуют "наихудшей" аппроксимации, так как (1) при l= 0 и (2) при m= 0 имеют бесконечное число решений какими бы ни были a1, ..., an). Подобные связи существуют между однородной и неоднородной задачами (см. [1], [5]) и не только в случае линейных Д. п. Если, напр., a1; . . .. an таковы, что при любом e>0 для всех целых x>0

где С 1>0 зависит только от а 1, ..., an и е, то каковы бы ни были действительные числа b1, . . ., bn, при любом e1>0 система неравенств

имеет целое решение хс условием
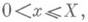 если Х>Х 0(a1, ..., an, e1). Более того, неравенство (3) обеспечивает "сильную" равномерную распределенность дробных долей ({a1, q}, ... , {anq}), где q=1,2, . . ., Q;число этих дробей, попадающих в систему интервалов
если Х>Х 0(a1, ..., an, e1). Более того, неравенство (3) обеспечивает "сильную" равномерную распределенность дробных долей ({a1, q}, ... , {anq}), где q=1,2, . . ., Q;число этих дробей, попадающих в систему интервалов  каждый из к-рых лежит внутри единичного интервала, равно
каждый из к-рых лежит внутри единичного интервала, равно 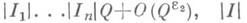 -
-длина интервала I, e2>0 - произвольно. Выполнение неравенства (3) для всех целых x>0 равносильно выполнению неравенства
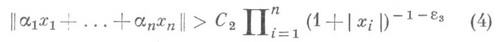
для всех целых
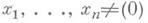 при любом e3>0, где С 2>0 зависит только от a1, . . ., an и e3.
при любом e3>0, где С 2>0 зависит только от a1, . . ., an и e3.Доказательство разрешимости или неразрешимости диофантовых неравенств, параметры к-рых определены арифметич. или аналитич. условиями, часто является весьма сложной задачей. Так, задача о приближениях алгебраич. чисел рациональными, систематически изучаемая со времени доказательства неравенства Лиувилля (1844) (см. Лиувилля число), до сих пор не получила полного решения (см. Туэ- Зигеля- Рота теорема, Диофамтовых приближений проблемы эффективизации). Доказано [11], что для алгебраич. чисел a1,. . .,an, вместе с 1 линейно независимых над полем рациональных чисел, выполняются неравенства (3), (4) при любых e>0, e3>0. Из этого следует, что система неравенств (1) при любом l>0 и система неравенств (2) при любом m>0 имеют лишь конечное число решений. Существует тесная связь между подобными теоремами о Д. п. к алгебраич. числам и представлением целых чисел неполными разложимыми формами. В частности, задача о границах для решений х, у диофантова уравнения Туэ f(x,y)=A при фиксированной целочисленной неприводимой бинарной форме f(x, у )не менее чем 3-й степени и переменном целом Аравносильна изучению рациональных приближений к корню aмногочлена f(x,1). Таким путем А. Туэ (А. Thue) доказал конечность числа решений уравнения f(x, y) = A, предварительно получив нетривиальную оценку рациональных приближений к a. Этот подход, обобщенный и развитый К. Зигелем (С. Siegel), привел его к теореме о конечности числа целых точек на алгебраич. кривых рода больше нуля (см. Диофантова геометрия). В. Шмидт [11] использовал подобные идеи для полного решения задачи о представлении чисел разложимыми формами, основываясь на своих аппроксимационных теоремах. В нек-рых случаях связи между теорией Д. п. и теорией диофантовых уравнений не столь непосредственны, хотя законы аппроксимации чисел могут играть главную роль в доказательствах существования решении, асимптотики числа решений и т. п. (задачи типа Варима проблемы и метод Харди - Литлвуда - Виноградова).
Д. п. к специальным числам, заданным как значения трансцендентных функций в рациональных или алгебраич. точках, изучаются методами теории трансцендентных чисел. Как правило, доказательство иррациональности или трансцендентности к.-л. числа позволяет дать оценку аппроксимации его рациональными или алгебраич. числами. Для трансцендентного aвеличину wn(a, H)=min|Р(a)|, где минимум берется по всем ненулевым целочисленным многочленам степени не более пи высоты не более Н, наз. мерой трансцендентности числа a. Оценка снизу величины wn(a, H), главным образом при фиксированном пи переменном Н, составляет содержание многих теорем теории трансцендентных чисел (см. [12]). Напр., К. Малер ([7], [12]) доказал, что

где С 3>0 - абсолютная постоянная, Н>Н 0 (п). Другим методом А. Бейкер [3] доказал (4) для различных не равных нулю рациональных степеней ес
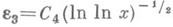 , где
, где
зависит только от п,a1, ..., an. Так как величина wn(a, H )будет "малой" лишь тогда, когда хотя бы одно алгебраич. число степени не более пи высоты не более Н"близко" к а, то существует связь между оценкой величины wn(a, H )и оценкой аппроксимации a алгебраич. числами степени не более п. Пусть w*n(a, H)=min |a- х|, где минимум берется по всем алгебраич. числам x, степени не более пи высоты не более Н, и пусть

Э. Вирзинг [13] нашел соотношения между величинами wn(a, Н )и w*(a, Н)(a - действительное)

В частности, если wn(a)=n, то w*n(a) = n, и так как
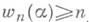 для всех трансцендентных а, то w*n(a)
для всех трансцендентных а, то w*n(a) (n+l)/2. Из последнего следует, что для всякого трансцендентного асуществует бесконечное число алгебраич. х степени не более п, удовлетворяющих неравенству
(n+l)/2. Из последнего следует, что для всякого трансцендентного асуществует бесконечное число алгебраич. х степени не более п, удовлетворяющих неравенству 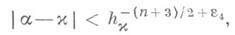 где hx,- высота x, e4>0 - произвольно. Э. Вирзинг высказал предположение, что
где hx,- высота x, e4>0 - произвольно. Э. Вирзинг высказал предположение, что 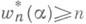 для всех трансцендентных a. и всех n=1, 2, .... Кроме очевидного случая n=1 эта гипотеза доказана для n=2 (см. [4]). Известно также, что для почти всех (в смысле меры Лебега) действительных а верны равенства
для всех трансцендентных a. и всех n=1, 2, .... Кроме очевидного случая n=1 эта гипотеза доказана для n=2 (см. [4]). Известно также, что для почти всех (в смысле меры Лебега) действительных а верны равенства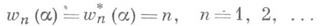
(см. [2], Метрическая теория чисел, Диофантовых приближений метрическая теория).
Изучение диофантовых уравнений методами р-адического анализа стимулировало развитие теории Д. п. в поле р-адических чисел Q р, к-рая строится во многом параллельно теории Д. п. в поле действительных чисел, но с учетом неархимедовой топологии поля Q р. Напр., пусть
 - р-адическое число. Рассматривая приближения нуля (в р-адической метрике) значениями целочисленной линейной формы w х+y, приходят к рациональным приближениям со, к-рые, подобно случаю действительных чисел, тесно связаны с разложением со в цепную (р-адическую) дробь [10]. Справедливы аналоги теорем Дирихле, Кронекера, Минковского и т. п., метрич. теорем,, теорем о приближениях алгебраич. числами и т. д. [2], [6], [8]. Диофантовы неравенства в Qp можно интерпретировать как сравнения по "высокой" степени р, что дает иногда возможность получать чисто арифметич. теоремы аналитич. методом. Глубокое развитие Д. п. в поле Q р и его конечных расширениях позволяет использовать метод Туэ - Зигеля - Рота для доказательства теорем об арифметич. структуре чисел, представимых бинарными формами, об оценке дробных долей степеней рациональных чисел и т. п. (см. [10]).
- р-адическое число. Рассматривая приближения нуля (в р-адической метрике) значениями целочисленной линейной формы w х+y, приходят к рациональным приближениям со, к-рые, подобно случаю действительных чисел, тесно связаны с разложением со в цепную (р-адическую) дробь [10]. Справедливы аналоги теорем Дирихле, Кронекера, Минковского и т. п., метрич. теорем,, теорем о приближениях алгебраич. числами и т. д. [2], [6], [8]. Диофантовы неравенства в Qp можно интерпретировать как сравнения по "высокой" степени р, что дает иногда возможность получать чисто арифметич. теоремы аналитич. методом. Глубокое развитие Д. п. в поле Q р и его конечных расширениях позволяет использовать метод Туэ - Зигеля - Рота для доказательства теорем об арифметич. структуре чисел, представимых бинарными формами, об оценке дробных долей степеней рациональных чисел и т. п. (см. [10]).Так как разложение функций в непрерывные дроби осуществляется аналогично разложению чисел в цепные дроби, то естественно возникает дальнейшая аналогия: приближение функций рациональными функциями в метрике поля степенных рядов. Этот подход имеет далекое развитие и приводит к теории Д. п. в поле степенных рядов. Пусть К- произвольное алгебраич. поле, К[х] - кольцо многочленов от хнад К, К( х -1)- поле степенных рядов вида
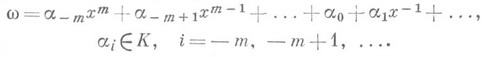
В поле К( х -1 )вводится неархимедово нормирование
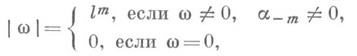
где Z>1 - произвольное фиксированное число. Поле К {х -1 )с нормированием |w| становится метрич. пространством. Изучение "диофантовых" приближений осуществляется по обычной схеме, где К[х]играет роль кольца целых чисел: рассматриваются аппроксимирующие функций со значениями в К( х -1 )от конечного числа переменных со значениями в К[х], а близость к нулю оценивается с помощью введенного нормирования. Есть определенное сходство получаемых таким путем результатов со случаем Д. п. в поле действительных чисел, но если К( х -1 )заменить полем К(х)рядов вида
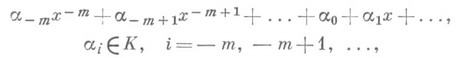
то результаты будут аналогичны приближениям в поле р-адических чисел (см. [2], [9]).
Д. п. в поле степенных рядов в несколько более конкретной форме (специализации К, явная оценка точности приближения и т. п.) составляют основу нек-рых аналитич. методов теории трансцендентных чисел.
В развитии теории Д. п. выделяются три подхода: глобальный, метрический и индивидуальный. При глобальном подходе изучаются общие законы аппроксимации, справедливые для всех чисел или для всех за "редким" исключением. Сюда относятся теорема Дирихле об однородных приближениях, теорема Кронекера о неоднородных приближениях, общие теоремы о приближении чисел алгебраическими, классификации чисел по аппроксимационным свойствам и т. п. Соответственно применяемые методы носят "глобальный" характер (непрерывные дроби, применения теоремы Минковского и методы геометрии чисел и т. п.). Метрич. подход требует описания аппроксимационных свойств чисел на основе понятий теории меры (см. Диофантовых приближений метрическая теория, Метрическая теория чисел). Получаемые результаты касаются не всех, а почти всех (в смысле определенной меры) чисел из рассматриваемых множеств или описываются с помощью нек-рой метрич. характеристики (размерность Хаусдорфа, емкость и т. п.). Применяемые методы тесно связаны с теорией меры, теорией вероятностей и смежными дисциплинами. Индивидуальный подход касается аппроксимационных свойств специальных чисел (алгебраич. числа, е,p, In 2 и т. п.) или требует построения чисел с определенными аппроксимационными свойствами (числа Лиувилля, T-числа Малера и т. п.). Методы решения таких задач специфичны и часто создаются специально для анализа конкретной задачи.
Лит.:[1] Касселс Дж. B.C., Введение в теорию дпофантовых приближений, пер. с англ., М., 1961; [ 2] Спринджук В. Г., Проблема Малера в метрической теории чисел, Минск, 1967; [3] Baker A., "Canad. J. Math.", 1965, v. 17, p. 616-26; [4] Davenport H., SchmidtW., "Acta Arithm.", 1967, v. 13, p. 169-76; [5] Koksma J. F., Diophantische Approximationen, В., 1936; [6] Lutz E., Sur les approximations diophantiennes lineaires p-adiques, P., 1955; [7] Mahler K., "Math. Z.", 1930, Bd 31, S. 729-32; [8] его жe, "Jahresber. DMV", 1934, Bd 44, S. 250-55; [9] его же, "Ann. Math.", 1941, v. 42, p. 488-522; [10] его же, Lectures on Diophantine approximations [s. 1.], pt 1, 1961; [11] Schmidt W., "L'enseignment Math. Revue intern., ser. 2", 1971, v. 17, №3-4, p. 187-253; [12] Schneider Th., Einfuhrung in die transzendenten Zahlen, В., 1957; [13] Wirsing E., "J. reine und angew. Math.", 1961, Bd 206, № 1-2, S. 67-77.
В. Г. Спринджук.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
