- АНАЛИТИЧЕСКИЙ ВЕКТОР
в пространстве V представления Тгруппы Л и G - вектор
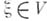 , для к-рого отображение
, для к-рого отображение  является вещественно аналнтич. вектор-функцией на Gсо значениями в Т" (см. Представлений теория). Если Т - слабо непрерывное представление группы Ли Gв банаховом пространстве V, то множество Vw аналитич. векторов плотно в V(см. [1], [2], [3]). Существует обобщение этой теоремы на широкий класс представлений в локально выпуклых пространствах [5]. Было доказано [6], что представление связной группы Ли G в банаховом пространстве Vоднозначно восстанавливается по соответствующему представлению алгебры Ли группы
является вещественно аналнтич. вектор-функцией на Gсо значениями в Т" (см. Представлений теория). Если Т - слабо непрерывное представление группы Ли Gв банаховом пространстве V, то множество Vw аналитич. векторов плотно в V(см. [1], [2], [3]). Существует обобщение этой теоремы на широкий класс представлений в локально выпуклых пространствах [5]. Было доказано [6], что представление связной группы Ли G в банаховом пространстве Vоднозначно восстанавливается по соответствующему представлению алгебры Ли группы  в пространстве
в пространстве  .
.
Аналитический вектор для неограниченного оператора
 в банаховом пространстве
в банаховом пространстве  с областью определения
с областью определения  определяется как вектор
определяется как вектор
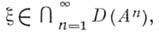
для к-рого ряд

имеет положительный радиус сходимости. Это понятие, введенное в [2], является частным случаем общего понятия А. в.- здесь в качестве группы Ли G выступает множество точек действительной прямой с операцией сложения. Оно оказалось полезным в теории операторов в банаховых пространствах и в теории эл-липтич. дифференциальных операторов.
Лит.:[1] Сartier P., Dixmier J., "Amer. J. Math.", 1958, v. 80, p. 131-45; [2] Hелсон Э., "Математика", 1962, 6 : 3, с. 89-131; [3] Гординг Л., "Математика", 1965, 9 : 5, с. 78-94; [4] Саrtiеr P., Vecteurs analytiques. Seminaire Bourbaki, Mai 1959; [5] Мооrе R. Т., "Memoirs Amer. Math. Soc.", 1968, v. 78; [6] Harish-Chandra, "Trans. Amer. Math. Soc.", 1953, v. 75, p. 185-243. А. А. Кириллов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
