- Критерий Пирсона
-
Критерий Пирсона, или критерий χ2 — наиболее часто употребляемый критерий для проверки гипотезы о законе распределения. Во многих практических задачах точный закон распределения неизвестен, то есть является гипотезой, которая требует статистической проверки.
Обозначим через X исследуемую случайную величину. Пусть требуется проверить гипотезу H0 о том, что эта случайная величина подчиняется закону распределения F(x). Для проверки гипотезы произведём выборку, состоящую из n независимых наблюдений над случайной величиной X. По выборке можно построить эмпирическое распределение F * (x) исследуемой случайной величины. Сравнение эмпирического F * (x) и теоретического распределений производится с помощью специально подобранной случайной величины — критерия согласия. Одним из таких критериев и является критерий Пирсона.
Содержание
Статистика критерия
Для проверки критерия вводится статистика:
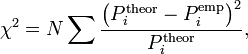
где
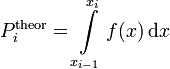 — предполагаемая вероятность попадения в i-й интервал,
— предполагаемая вероятность попадения в i-й интервал, 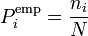 — соответствующее эмпирическое значение, ni — число элементов выборки из i-го интервала.
— соответствующее эмпирическое значение, ni — число элементов выборки из i-го интервала.Эта величина в свою очередь является случайной (в силу случайности X) и должна подчиняться распределению χ2.
Правило критерия
Перед тем, как сформулировать правило принятия или отвержения гипотезы необходимо учесть, что критерий Пирсона обладает правосторонней критической областью.

Правило.
Если полученная статистика превосходит квантиль закона распределения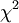 заданного уровня значимости
заданного уровня значимости 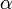 с
с 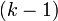 или с
или с 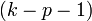 степенями свободы, где k — число наблюдений или число интервалов (для случая интервального вариационного ряда), а p — число оцениваемых параметров закона распределения, то гипотеза
степенями свободы, где k — число наблюдений или число интервалов (для случая интервального вариационного ряда), а p — число оцениваемых параметров закона распределения, то гипотеза 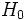 отвергается. В противном случае гипотеза принимается на заданном уровне значимости
отвергается. В противном случае гипотеза принимается на заданном уровне значимости 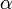 .
.Литература
- Кендалл М., Стьюарт А. Статистические выводы и связи. — М.: Наука, 1973.
См. также
- Критерий Пирсона на сайте Новосибирского государственного университета
- Критерии типа хи-квадрат на сайте Новосибирского государственного технического университета (Рекомендации по стандартизации Р 50.1.033–2001)
- О выборе числа интервалов на сайте Новосибирского государственного технического университета
- О критерии Никулина на сайте Новосибирского государственного технического университета
- Критерий согласия Колмогорова
- Критерий отношения правдоподобия
Wikimedia Foundation. 2010.
