Ковер Серпинского

Коврик Серпинского

Ковёр Серпинского — фрактал, один из двумерных аналогов множества Кантора предложенный польским математиком Вацлавом Серпинским. Также известен как квадрат Серпинского.

Построение

Берётся сплошной квадрат, разрезается на 9 равных квадратов и удаляется внутренность центрального квадрата. На втором шаге удаляется 8 центральных квадратов из 8 оставшихся квадратов и т. д. После бесконечного повторения этой процедуры, от сплошного квадрата остается замкнутое подмножество — коврик Серпинского.

Свойства

• Коврик Серпинского замкнут.
• Коврик Серпинского имеет топологическую размерность 1.
• Коврик Серпинского имеет промежуточную (то есть не целую) Хаусдорфову размерность 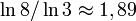$\ln8/\ln3\approx 1,89$. В частности,
  • имеет нулевую меру Лебега.

См. также

• Салфетка Серпинского (треугольник)
• Кривая Урысона
• Губка Менгера

Ссылки

• Медиафайлы по теме Ковёр Серпинского с Викисклада.
• Variations on the Theme of Tremas II (англ.)
• Печенье с рисунком-фракталом (англ.)