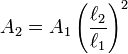Закон квадрата-куба

Закон квадрата - куба представляет собой принцип, применяемый в технике и биомеханике, и базируется на математическом пересчете размеров. Он был впервые продемонстрирован в 1638 г. Галилео Галилеем в "Discorsi e Dimostrazioni Matematiche, intorno a due nuove scienze («Беседы и математические доказательства двух новых наук»), 1638";. Он гласит

Когда объект подвергается пропорциональному увеличению размеров, его новый объем будет пропорционален кубу множителя, а новая площадь его поверхности пропорциональна квадрату множителя.

$v_2=v_1\left(\frac{\ell_2}{\ell_1}\right)^3$

где v₁ — объем исходного объекта, v₂ — новый объем, 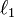$\ell_1$- линейный размер исходного объекта, а $\ell_2$ — новый линейный размер. Заметьте, что не имеет значения, какой линейный размер используется.

$A_2=A_1\left(\frac{\ell_2}{\ell_1}\right)^2$

где A₁ — площадь поверхности исходного объекта, а A₂ — новая площадь поверхности.

Например, куб с длиной стороны 1 метр имеет плошадь поверхности 6 м² и объем 1 м³. Если длину стороны удвоить, площадь его поверхности увеличится до 24 м², а его объем увеличится до 8 м³. Этот принцип применим ко всем телам.

Применения

Техника

Если физический объект увеличить в размерах при сохранении неизменной плотности материала, из которого он изготовлен, его масса увеличится в третьей степени, в то время как площадь его поверхности — только в квадрате масштабного множителя. Это должно означать, что в том случае, если увеличенному в размерах объекту сообщить то же ускорение, что и оригиналу, на поверхность увеличившегося объекта будет действовать большее давление

Давайте рассмотрим простой пример — тело массой = M имеет ускорение = a и площадь поверхности = A , на которую действует ускоряющая сила.

Сила, вызванная ускорением: F = M*a, а давление на поверхность T = F/A = M*a/A

Теперь рассмотрим объект, размеры которого умножены на коэффициент = x так, чтобы его новая масса M' = x3*M, а поверхность, на которую действует сила, имеет новую площадь, A' = x2*A.

Новая сила, вызванная ускорением F' = x³*M*a и

Результирующее давление на поверхность

                          T' = F'/A'
                                = x3*M*a/(x2*A)
                                = x*(M*a/A)
                                = x*T

Таким образом, при простом увеличении размеров объекта с сохранением того же самого материала конструкции (плотности), и при же самом ускорении, давление, производимое им на повехность, увеличится во столько же раз. Это показывает, что способность сопротивляться напряжению у объекта снизится и он станет более склонен к разрушению в процессе ускорения.

Это и есть объяснение тому, почему большие транспортные средства плохо выдерживают испытания на разрушения при столкновениях и почему есть пределы высоты строительства высотных зданий. Аналогично, чем больше размер объекта, тем меньше другие объекты окажут сопротивление движению, вызывая его замедление

Биомеханика

Если размеры животного значительно увеличить, его мускульная сила серьезно уменьшится, так как поперечное сечение его мускулов увеличится пропорционально площади коэффициента масштабирования, в то время как его масса увеличится пропорционально кубу коэффициента масштабирования. В результате этого сердечно-сосудистые функции сильно ограничатся. Для летающих животных, если их увеличить в размерах, их нагрузка на крылья должна возрасти, и поэтому им, чтобы совершать такой же взлет, придется лететь быстрее,. Это будет нелегко ввиду того, что сила мускулов станет меньше. Это также объясняет, почему шмель может иметь большой размер тела относительно размаха его крыльев, что невозможно для большего летающего животного. Для животных малых размеров сопротивление воздуха на единицу массы также выше, что объясняет, отчего маленькое насекомое, такое, как муравей не погибнет, падая с любой высоты, а экипаж танка, также как и слон, не сможет выжить при падении с высоты в одну милю

По этой причине гигантские насекомые, пауки и другие животные, показываемые в фильмах ужасов — нереальны, поскольку такие крутые размеры вызвали бы их разрушение. Исключением являются гигантские водные животные, поскольку вода способна поддерживать такие огромные существа.

Данная статья статья представляет собой несколько доработанный перевод статьи из английской Википедии

Square-Cube Law

См. также

Биомеханика

Allometric law (англ.)

On Being the Right Size (англ.)

Ссылки

Wayne Throop. «Sauropods, Elephants, Weightlifters: Miscellaneous Issues» (англ.).

«World Builders: The Limits to Animal Size — Size to Volume Ratio». (англ.)

Michael C. LaBarbera. «The Biology of B-Movie Monsters»(англ.)