- Задача ВЫП
-
Задача выполнимости булевых формул (SAT или ВЫП) — задача распознавания, важная для теории вычислительной сложности.
Экземпляром задачи SAT является булева формула, состоящая только из имен переменных, скобок и операций
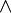 (И),
(И), 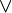 (ИЛИ) и
(ИЛИ) и  (HE). Задача заключается в следующем: можно ли назначить всем переменным, встречающимся в формуле, значения ЛОЖЬ и ИСТИНА так, чтобы формула стала истинной.
(HE). Задача заключается в следующем: можно ли назначить всем переменным, встречающимся в формуле, значения ЛОЖЬ и ИСТИНА так, чтобы формула стала истинной.Согласно теореме Кука, доказанной Стивеном Куком в 1971-м году, задача SAT NP-полна.
Содержание
Точная формулировка
Чтобы четко сформулировать задачу распознавания, необходимо условиться об алфавите, с помощью которого задаются экземпляры языка. Этот алфавит должен быть фиксирован и конечен. В своей книге Хопкрофт, Мотвани и Ульман предлагают использовать следующий алфавит: {«
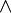 », «
», «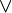 », «
», « », «(», «)», «x», «0», «1»}.
», «(», «)», «x», «0», «1»}.При использовании такого алфавита скобки и операторы записываются естественным образом, а переменные получают следующие имена: x1, x10, x11, x100 и т. д., согласно их номерам, записанным в двоичной системе счисления.
Пусть некоторая булева формула, записанная в обычной математической нотации, имела длину N символов. В ней каждое вхождение каждой переменной было описано хотя бы одним символом, следовательно, всего в данной формуле не более N переменных. Значит, в предложенной выше нотации каждая переменная будет записана с помощью
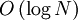 символов. В таком случае, вся формула в новой нотации будет иметь длину
символов. В таком случае, вся формула в новой нотации будет иметь длину 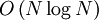 символов, то есть длина строки возрастет в полиномиальное число раз.
символов, то есть длина строки возрастет в полиномиальное число раз.Например, формула
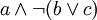 примет вид
примет вид 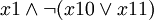 .
.Вычислительная сложность
В 1971-м году в статье Стивена Кука был впервые введен термин «NP-полная задача», и задача SAT была первой задачей, для которой доказывалось это свойство.
В доказательстве теоремы Кука каждая задача из класса NP в явном виде сводится к SAT. После появления результатов Кука была доказана NP-полнота для множества других задач. При этом чаще всего для доказательства NP-полноты некоторой задачи приводится полиномиальное сведение задачи SAT к данной задаче, возможно в несколько шагов, то есть с использованием нескольких промежуточных задач.
Частные случаи задачи SAT
Интересными важными частными случаями задачи SAT являются:
- Задача выполнимости булевых формул в конъюнктивной нормальной форме (SATCNF или ВКНФ) — аналогичная задача, с наложенной на формулу условием: она должна быть записана в конъюнктивной нормальной форме. Задача ВКНФ также NP-полна.
- Задача выполнимости булевых формул в k-конъюнктивной нормальной форме (k-SAT или k-ВЫП) — задача выполнимости при условии, что формула записана в k-конъюнктивной нормальной форме. Эта задача является NP-полной при
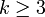 .
. - Задача выполнимости булевых формул в 2-конъюнктивной нормальной форме имеет полиномиальное решение, то есть принадлежит классу P.
См. также
Ссылки
Примечания
NP-полные (трудные) задачи Теория сложности вычислений Упаковка, укладка Упаковка в контейнеры: двумерная упаковка • линейная упаковка • упаковка по весу • упаковка по стоимости
Задача о ранце (рюкзаке)Булева формула Задача выполнимости булевых формул Коммивояжёр Задача коммивояжёра Вершинное покрытие Задача о вершинном покрытии Клика Задача о клике Независимое множество Задача о независимом множестве (наборе) Покрытие множества Задача о покрытии множества Латинский квадрат Задача о заполнении латинского квадрата Обобщённое судоку Задача обобщённого судоку Какуро Задача какуро Пятнашки (обобщённые) Задача поиска кратчайшего решения (костяшек более 15) Классы сложности
Wikimedia Foundation. 2010.
