Жесткость (геометрия)

Жёсткость — свойство подмногообразия M в евклидовом пространстве (или, более обще, в пространстве постоянной кривизны), заключающееся в том, что любая его изометрическая вариация (бесконечно малое изгибание) является тривиальной, то есть соответствующее её поле скоростей на M индуцируется полем Киллинга на M. Вопрос о жёсткости подмногообразий — по существу вопрос о единственности решения системы дифференциальных уравнений, являющихся линеаризацией системы уравнений для изометричных изгибаний подмногообразия. В частности, если подмногообразие допускает нетривиальное изометрические изгибание то оно не является жёстким.

Примеры

• Замкнутая строго выпуклая поверхность — жёсткая.
• Тор — жёсткий.
• Кусок плоскости с закрепленным краем — нежёсткий.
• Сферический сегмент S, скользящий краем по плоскости, будет жестким или нет в зависимости от того, меньше или больше S полусферы.
• Метрическое произведение k двумерных сфер 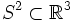$S^2\subset \mathbb R^{3}$ является жёстким в евклидовом пространстве $\mathbb R^{3k}$ и нежёстким в $\mathbb R^{3k + 1}$.

Вариации

Понятие жёсткости переносится также на многогранники, см. теорема Коши о многогранниках.