- Двойной интеграл
-
В математическом анализе кратным или многократным интегралом называют множество интегралов взятых от
 переменных. Например:
переменных. Например: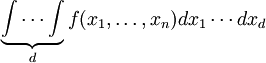
Замечание: кратный интеграл − это определенный интеграл, при его вычислении всегда получается число.
Содержание
Определение кратного интеграла
Определение на
 языке
языкеКратным интегралом (n-кратным) функции f на компакте B называется число I (если оно существует), такое что
 , такое что
, такое что 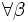 (разбиение) с
(разбиение) с 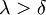 и любого выбора точек выполняется:
и любого выбора точек выполняется: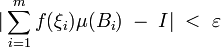 .
.Определение с использованием интегральных сумм
Пусть множество
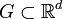 измеримо, функция
измеримо, функция 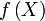 определена на
определена на 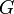 . Рассмотрим разбиение множества
. Рассмотрим разбиение множества 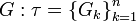 .
.1)
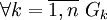 измеримо,
измеримо,2)
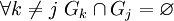 ,
,3)
 .
.Введем
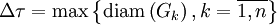 — мелкость разбиения
— мелкость разбиения 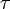 ,
, 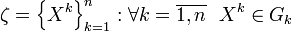 — набор промежуточных точек.
— набор промежуточных точек.Рассмотрим интегральную сумму
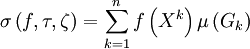 , где
, где 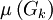 есть мера
есть мера 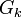 .
.Если существует конечный предел
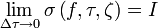 , то говорят, что
, то говорят, что 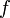 интегрируема по Риману на множестве
интегрируема по Риману на множестве 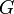 , и обозначают этот факт следующим образом:
, и обозначают этот факт следующим образом:1) В векторном виде:
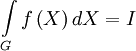 ,
,2) Либо ставят значок интеграла
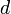 раз, записывают функцию и
раз, записывают функцию и 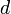 дифференциалов:
дифференциалов: 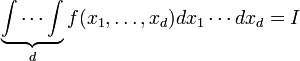 .
.Существование кратного интеграла
Достаточные условия
- Если функция непрерывна на измеримом по Жордану компакте, то она интегрируема на нем.
- Если функция определена на измеримом по Жордану множестве, у которого существуют сколь угодно мелкие разбиения, для которых данная функция неограничена на объединении всех их элементов положительной меры, то эта функция неинтегрируема на этом множестве.
Критерий Дарбу
Свойства кратных интегралов
Линейность по функции
Пусть
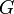 измеримо, функции
измеримо, функции 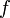 и
и  интегрируемы на
интегрируемы на 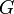 , тогда
, тогда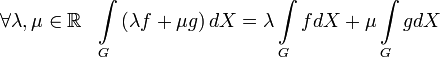 .
.Аддитивность по множеству интегрирования
Пусть множества
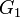 и
и  измеримы,
измеримы, 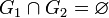 и
и 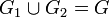 . Пусть также функция
. Пусть также функция 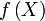 определена и интегрируема на каждом из множеств
определена и интегрируема на каждом из множеств 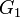 и
и 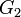 . Тогда
. Тогда .
.Сохранение неравенств при интегрировании
Пусть
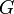 измеримо, функции
измеримо, функции 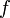 и
и  интегрируемы на
интегрируемы на 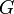 , причем
, причем  . Тогда
. Тогда 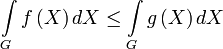 .
.Интегральное неравенство треугольника
Следствие предыдущего свойства.
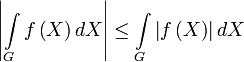
Интегральная теорема о среднем
Пусть
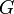 — компакт, функция
— компакт, функция 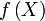 непрерывна и интегрируема на
непрерывна и интегрируема на 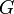 , тогда
, тогда 
Прочие свойства
1) Если
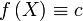 , то она интегрируема на любом измеримом множестве
, то она интегрируема на любом измеримом множестве 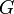 , причем
, причем  .
.2) Следствие 1).
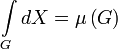 .
.Вычисление кратных интегралов
Сведение кратного интеграла к повторным
Пусть
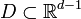 — измеримое множество,
— измеримое множество, 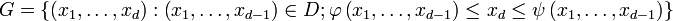 — также измеримое множество,
— также измеримое множество, 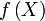 определена и интегрируема на
определена и интегрируема на 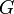 . Тогда
. Тогда![\int\limits_{G}{f\left( {{x}_{1}},\ldots ,{{x}_{d}} \right)d{{x}_{1}}\ldots d{{x}_{d}}}=\int\limits_{D}{\left[ \int\limits_{\varphi \left( {{x}_{1}},\ldots ,{{x}_{d-1}} \right)}^{\psi \left( {{x}_{1}},\ldots ,{{x}_{d-1}} \right)}{f\left( {{x}_{1}},\ldots ,{{x}_{d}} \right)d{{x}_{d}}} \right]d{{x}_{1}}\ldots d{{x}_{d-1}}}](/pictures/wiki/files/98/b0740514ef67d5a177794a0bcd4c1fea.png) .
.Любой d-мерный интеграл можно свести к d одномерным.
Замена переменных в кратном интеграле
Пусть у нас задано биективное отображение
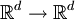 , переводящее область
, переводящее область 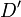 в
в  :
: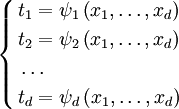 ,
,где t — «старые» координаты, а x — «новые» координаты. Пусть также функции, задающие отображение, имеют в области
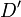 непрерывные частные производные первого порядка и отличный от нуля Якобиан
непрерывные частные производные первого порядка и отличный от нуля Якобиан 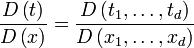 . Тогда при условии существования интеграла
. Тогда при условии существования интеграла  справедлива формула замены переменных:
справедлива формула замены переменных: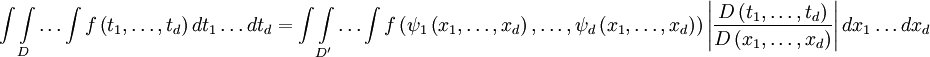
Двойной интеграл
 Геометрический смысл двойного интеграла
Геометрический смысл двойного интегралаДвойным интегралом называют кратный интеграл с
 .
.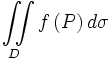 . Здесь
. Здесь 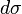 — элемент площади в рассматриваемых координатах.
— элемент площади в рассматриваемых координатах.В прямоугольных координатах:
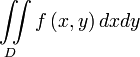 , где
, где 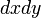 — элемент площади в прямоугольных координатах.
— элемент площади в прямоугольных координатах.Геометрический смысл двойного интеграла
Пусть функция
 принимает в области
принимает в области  только положительные значения. Тогда двойной интеграл
только положительные значения. Тогда двойной интеграл 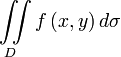 численно равен объему
численно равен объему 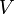 вертикального цилиндрического тела, построенного на основании
вертикального цилиндрического тела, построенного на основании  и ограниченного сверху соответствующим куском поверхности
и ограниченного сверху соответствующим куском поверхности 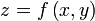 .
.Выражение двойного интеграла через полярные координаты
 Переход из прямоугольных координат в полярные.
Переход из прямоугольных координат в полярные. Переход из прямоугольных координат в полярные.
Переход из прямоугольных координат в полярные.В некоторых случаях двойной интеграл проще считать не в прямоугольных, а в полярных координатах, так как при этом может произойти существенное упрощение вида области интегрирования и всего процесса интегрирования в целом.
Применим теорему о замене переменных. Соответствующее переходу преобразование имеет вид:

Модуль якобиана отображения равен
 . Таким образом получаем, что
. Таким образом получаем, что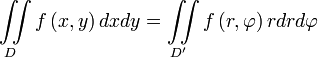 .
.Здесь
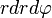 является элементом площади в полярных координатах.
является элементом площади в полярных координатах.Пример перехода в произвольную систему координат
Посчитаем площадь области
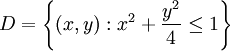 .
.Переход в полярную систему координат не сделает область проще:
 .
.
Множитель перед синусом «мешает». В этом случае переход можно немного скорректировать:
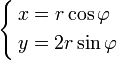 .
.
Это преобразование переведет исходную область в следующую:
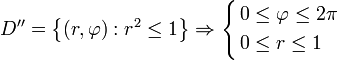 .
.
Якобиан отображения:
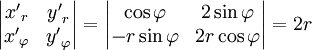 .
.
Модуль Якобиана также равен 2r.
Отсюда
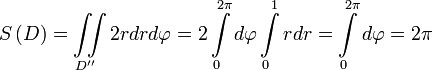 .
.
Результат верный, так как область
 ограничена эллипсом, заданным каноническим уравнением. Площадь можно посчитать по формуле S = πab. Путем подстановки убеждаемся в верности вычисления интеграла.
ограничена эллипсом, заданным каноническим уравнением. Площадь можно посчитать по формуле S = πab. Путем подстановки убеждаемся в верности вычисления интеграла.Приложения двойных интегралов
Наименование величины Общее выражение Прямоугольные координаты Полярные координаты Площадь плоской фигуры 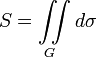
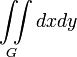
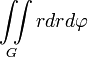
Масса тонкой плоской пластинки плотностью μ
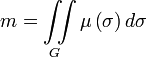
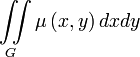
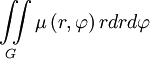
Площадь куска поверхности1) 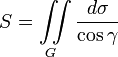
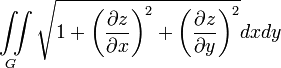
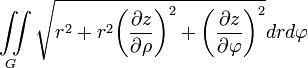
Объем цилиндрического тела, стоящего на плоскости XOY
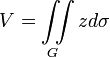
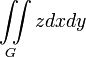
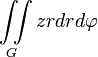
Момент инерции плоской фигуры2) относительно оси OZ3)
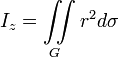
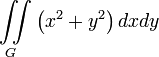
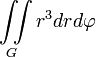
Момент инерции плоской фигуры2) относительно оси OX3)


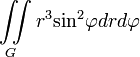
Координаты центра тяжести однородной пластинки3)
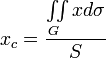

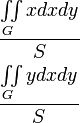
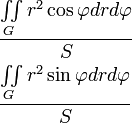
Примечания 1) Область G — проекция на плоскость XOY; в каждую точку области проектируется только одна точка поверхности;
γ — угол между касательной плоскостью и плоскостью XOY.
2) Совмещенной с плоскостью XOY.
3) Или, что то же, относительно центра О.
Тройной интеграл
Тройным интегралом называют кратный интеграл с
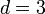 .
. Здесь
Здесь 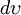 — элемент объема в рассматриваемых координатах.
— элемент объема в рассматриваемых координатах.В прямоугольных координатах
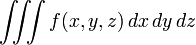 , где
, где 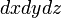 является элементом объема в прямоугольных координатах.
является элементом объема в прямоугольных координатах.Выражение тройного интеграла через цилиндрические координаты
 Объем в цилиндрических координатах
Объем в цилиндрических координатахАналогично в некоторых случаях тройной интеграл проще считать не в прямоугольных, а в цилиндрических координатах. Применим теорему о замене переменных. Соответствующее переходу преобразование имеет вид:
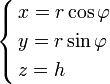
Модуль якобиана отображения равен
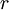 . Таким образом получаем, что
. Таким образом получаем, что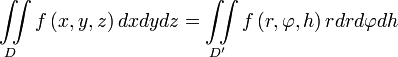
Здесь
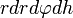 является элементом объема в цилиндрических координатах.
является элементом объема в цилиндрических координатах.Выражение тройного интеграла через сферические координаты
 Объем в сферических координатах
Объем в сферических координатахКроме цилиндрических можно также переходить и в сферические координаты. Применим теорему о замене переменных. Соответствующее переходу преобразование имеет вид:
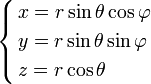
Модуль якобиана отображения равен
 . Таким образом получаем, что
. Таким образом получаем, что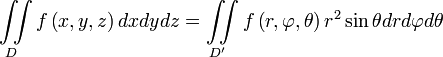
Здесь
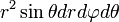 является элементом объема в цилиндрических координатах.
является элементом объема в цилиндрических координатах.Приложения тройных интегралов
Наименование величины Общее выражение Прямоугольные координаты Цилиндрические координаты Сферические координаты Объем тела 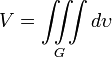
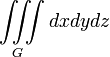
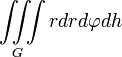
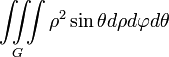
Момент инерции геометрического тела относительно оси OZ
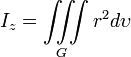
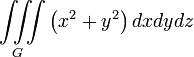
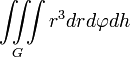
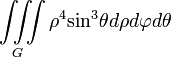
Масса физического тела с плотностью μ 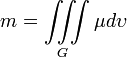


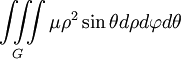
Координаты центра тяжести однородного тела


— — См. также
Литература
- Выгодский, М. Я. Дифференциирование и интегрирований функций нескольких аргументов // Справочник по высшей математике. — М.: Астрель, АСТ, 2005. — 991 с. — 10000 экз. — ISBN 5-17-012238-1, 5-271-03651-0
- Ильин, В. А., Позняк, Э. Г. Глава 2. Двойные и n-кратные интегралы // Основы математического анализа. — 4. — М.: ФИЗМАТЛИТ, 2002. — Т. 2. — 464 с. — (Курс высшей математики и математической физики). — 5000 экз. — ISBN 5-9221-0131-5
- Кудрявцев, Л. Д. Глава 6. Интегральное исчислений функций многих переменных // Курс математического анализа. — М.: Высшая школа, 1981. — Т. 2. — 584 с.
Wikimedia Foundation. 2010.
