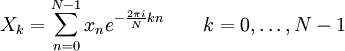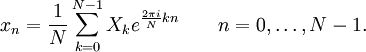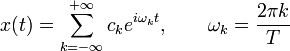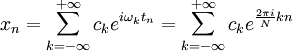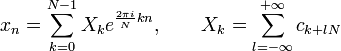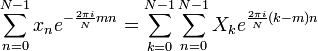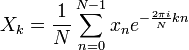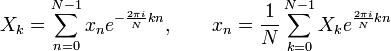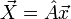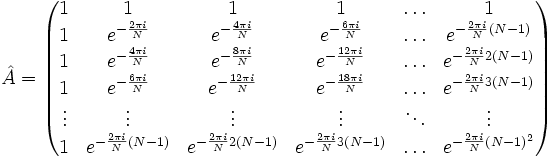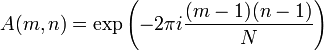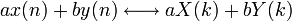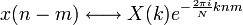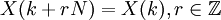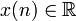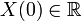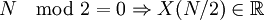ДПФ

Дискретное преобразование Фурье (в англоязычной литературе DFT, Discrete Fourier Transform) — это одно из преобразований Фурье, широко применяемых в алгоритмах цифровой обработки сигналов (его модификации применяются в сжатии звука в jpg и др.), а также в других областях, связанных с анализом частот в дискретном (к примеру, оцифрованном аналоговом) сигнале. Также дискретные преобразования Фурье помогают решать частные дифференциальные уравнения и выполнять такие операции, как свёртки. Преобразования бывают одномерные, двумерные и даже трехмерные.

Последовательность N комплексных чисел x₀, …, x_N−1 преобразуется в последовательность из N комплексных чисел X₀, …, X_N−1 с помощью дискретного преобразования Фурье по формуле:

$X_k = \sum_{n=0}^{N-1} x_n e^{-\frac{2 \pi i}{N} k n} \qquad k = 0, \dots, N-1$

где i — это мнимая единица. Обратное дискретное преобразование Фурье задается формулой

$x_n = \frac{1}{N} \sum_{k=0}^{N-1} X_k e^{\frac{2\pi i}{N} k n} \quad \quad n = 0,\dots,N-1.$

Поскольку напрямую вычисления дискретного преобразования требует O(N²) операций, то на практике используют более быстрый алгоритм Быстрого преобразования Фурье, которое требует O(NlogN) операций.

Вывод преобразования

Рассмотрим некоторый периодический сигнал x(t) c периодом равным T. Разложим его в ряд Фурье:

$x(t) = \sum_{k=-\infty}^{+\infty} c_k e^{i\omega_k t}, \qquad \omega_k = \frac{2\pi k}{T}$

Проведем дискретизацию сигнала так, чтобы на периоде было N отсчетов. Дискретный сигнал представим в виде отсчетов: x_n = x(t_n), где 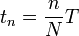$t_n = \frac nN T$, тогда ряд Фурье запишется следующим образом:

$x_n = \sum_{k=-\infty}^{+\infty} c_k e^{i\omega_k t_n} = \sum_{k=-\infty}^{+\infty} c_k e^{\frac {2\pi i}{N} kn}$

Используя соотношение: 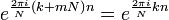$e ^{\frac{2\pi i}{N} \left(k+mN \right)n} = e ^{\frac{2\pi i}{N} kn}$, получаем:

$x_n = \sum_{k=0}^{N-1} X_k e ^{\frac{2\pi i}{N} kn}, \qquad X_k = \sum_{l=-\infty}^{+\infty} c_{k+lN}$

Таким образом мы получили обратное дискретное преобразование Фурье.

Умножим теперь скалярно выражение для x_n на 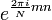$e^{\frac{2\pi i}{N} mn}$ и получим:

$\sum_{n=0}^{N-1}x_n e^{-\frac{2\pi i}{N} mn} = \sum_{k=0}^{N-1} \sum_{n=0}^{N-1} X_k e^{\frac{2\pi i}{N} (k-m)n}$

Откуда следует, что:

$X_k = \frac 1N \sum_{n=0}^{N-1} x_n e^{-\frac{2\pi i}{N} kn}$

Эта формула описывает прямое дискретное преобразование Фурье.

В литературе принято писать множитель 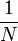$\frac{1}{N}$ в обратном преобразовании, и поэтому обычно пишут формулы преобразования в следующем виде:

$X_k = \sum_{n=0}^{N-1} x_n e^{-\frac{2\pi i}{N} kn}, \qquad x_n =\frac 1N \sum_{k=0}^{N-1} X_k e ^{\frac{2\pi i}{N} kn}$

Матричное представление

Дискретное преобразование Фурье является линейным преобразованием, которое переводит вектор временных отсчетов 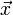$\vec x$ в вектор спектральных отсчетов той же длины. Таким образом преобразование может быть реализовано как умножение квадратной матрицы на вектор:

$\vec X = \hat A \vec x$

матрица А имеет вид:

$\hat A = \begin{pmatrix} 1 &1 &1 &1 &\ldots &1 \\ 1 &e^{-\frac{2\pi i}{N}} &e^{-\frac{4\pi i}{N}} &e^{-\frac{6\pi i}{N}} &\ldots &e^{-\frac{2\pi i}{N}(N-1)}\\ 1 &e^{-\frac{4\pi i}{N}} &e^{-\frac{8\pi i}{N}} &e^{-\frac{12\pi i}{N}} &\ldots &e^{-\frac{2\pi i}{N}2(N-1)}\\ 1 &e^{-\frac{6\pi i}{N}} &e^{-\frac{12\pi i}{N}} &e^{-\frac{18\pi i}{N}} &\ldots &e^{-\frac{2\pi i}{N}3(N-1)}\\ \vdots &\vdots &\vdots &\vdots &\ddots &\vdots\\ 1 &e^{-\frac{2\pi i}{N}(N-1)} &e^{-\frac{2\pi i}{N}2(N-1)} &e^{-\frac{2\pi i}{N}3(N-1)} &\ldots &e^{-\frac{2\pi i}{N}(N-1)^2} \end{pmatrix}$

Элементы матрицы задаются следующей формулой:

$A(m,n) = \exp \left( -2\pi i \frac{(m-1)(n-1)}{N} \right)$

Свойства

• 1) линейность

${ax(n)+by(n)} \longleftrightarrow {aX(k)+bY(k)}$

• 2) сдвиг по времени

${x(n-m)} \longleftrightarrow X(k)e^{-\frac{2 \pi i}{N} k n m}$

• 3) периодичность

$X(k+rN)=X(k), r \in \mathbb Z$

• 4) выполняется Теорема Парсеваля
• 5) симметрии

X(k) = X(N − k)

Таким образом информацию несут первые N/2 гармоник.

• 6) обладает спектральной плотностью

S(k) = | x(k) | ²

• 7)

$x(n) \in \mathbb R$

$X(0) \in \mathbb R$

$N \mod 2 = 0 \Rightarrow X(N/2) \in \mathbb R$

Стоит отметить, что нулевая гармоника является суммой значений сигнала.

См. также

• Преобразование Фурье
• Дискретное преобразование Хартли
• Дискретное преобразование Фурье над конечным полем
• Быстрое преобразование Фурье
• Дискретное комплексное преобразование
• Оконное преобразование Фурье

Литература

• Сергиенко А. Б. Цифровая обработка сигналов. — 2-е. — Спб: Питер, 2006. — С. 751. — ISBN 5-469-00816-9
• М. А. Павлейно, В. М. Ромаданов Спектральные преобразования в MatLab. — СПб: 2007. — С. 160. — ISBN 978-5-98340-121-1