- Оконное преобразование Фурье
-
Оконное преобразование Фурье — это разновидность преобразования Фурье, определяемая следующим образом:
где
 — некоторая оконная функция. В случае дискретного преобразования оконная функция используется аналогично:
— некоторая оконная функция. В случае дискретного преобразования оконная функция используется аналогично:Содержание
Применение
В большинстве задач цифровой обработки нет возможности исследовать сигнал на бесконечном интервале. Нет возможности узнать, какой был сигнал до включения устройства и какой он будет в будущем. Также ограничение интервала исследования может быть обусловлено нестационарностью исследуемого сигнала.
Ограничение интервала анализа равносильно произведению исходного сигнала на оконную функцию. Таким образом, результатом оконного преобразования Фурье является не спектр исходного сигнала, а спектр произведения сигнала и оконной функции. Спектр, полученный при помощи оконного преобразования Фурье, является оценкой спектра исходного сигнала и принципиально допускает искажения.
Искажения, вносимые применением окон, определяются размером окна и его формой. Выделяют два основных свойства частотных характеристик окон: ширина главного лепестка и максимальный уровень боковых лепестков. Применение окон, отличных от прямоугольного, обусловлено желанием уменьшить влияние боковых лепестков за счет увеличения ширины главного.
Частотно-временное разрешение
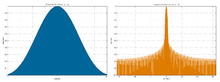
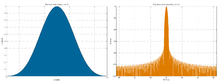
При использовании оконного преобразования Фурье невозможно одновременно обеспечить хорошее разрешение по времени и по частоте. Чем уже окно, тем выше разрешение по времени и ниже разрешение по частоте.
 Сравнение оконного преобразования Фурье с разными окнами. Слева (узкое окно) - хорошее разрешение по времени, справа (более широкое окно) - хорошее разрешение по частоте.
Сравнение оконного преобразования Фурье с разными окнами. Слева (узкое окно) - хорошее разрешение по времени, справа (более широкое окно) - хорошее разрешение по частоте.Разрешение по осям является постоянным. Это нежелательно для ряда задач, в которых информация по частотам распределена неравномерно. В таких задачах в качестве альтернативы оконному преобразованию Фурье может использоваться вейвлет-преобразование, временное разрешение которого увеличивается с частотой (частотное снижается).
Типы оконных функций
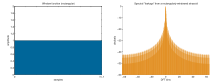
Прямоугольное окно
Получается автоматически при ограничении выборки N отсчетами. Максимальный уровень боковых лепестков частотной характеристики: -13 дБ.
Окно Ханна
где N — ширина окна. Уровень боковых лепестков: -31.5 дБ.
Окно Хемминга
Уровень боковых лепестков: -42 дБ.
Окно Блэкмана
Уровень боковых лепестков: -58 дБ (α=0.16).
Окно Кайзера
где
 — модифицированная функция Бесселя первого рода нулевого порядка;
— модифицированная функция Бесселя первого рода нулевого порядка;  — коэффициент определяющий долю энергии, сосредоточенной в главном лепестке спектра оконной функции. Чем больше
— коэффициент определяющий долю энергии, сосредоточенной в главном лепестке спектра оконной функции. Чем больше  тем больше доля энергии, и шире главный лепесток, и меньше уровень боковых лепестков. На практике используются значения от 4 до 9.
тем больше доля энергии, и шире главный лепесток, и меньше уровень боковых лепестков. На практике используются значения от 4 до 9.См. также
Внешние ссылки
- Некоторые оконные функции и их параметры
- Использование оконных функций в задачах цифрового спектрального анализа. Примеры и рекомендации
 Категории:
Категории:- Преобразование Фурье
- Цифровая обработка сигналов
Wikimedia Foundation. 2010.


![F(m,\omega) = \sum_{n=-\infty}^{\infty} f[n]w[n-m]e^{-j \omega n}](2f0613cffa1ce0e0d8297a72a312f8a2.png)
![w(n)=\left\{ \begin{matrix}
1 , & n\in[0,N-1] \\
0, & n\notin[0,N-1]\\
\end{matrix} \right.](e15ba420d6263c58adc5feaabf2bf362.png)