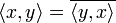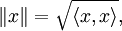- Внутреннее произведение
-
Внутреннее произведение — определённая на векторном пространстве L над полем K симметричная эрмитова форма, рассматриваемая обычно в качестве составной части определения этого пространства[1], делающей пространство (в зависимости от типа пространства и свойств внутреннего произведения[2]) предгильбертовым, гильбертовым, евклидовым, псевдоевклидовым и т. п.
Говорят, что на векторном пространстве (над полем в котором есть операция комплексного спряжения, обычно поле комплексных чисел, или поле реальных чисел, где операция комплексного спряжения есть операция эквивалентности) задано внутреннее произведение, если каждым двум векторам из этого пространства сопоставлено число (элемент того поля над которым построено векторное пространство), и удовлетворяет аксиомам:
1 - аксиомы линейности внутреннего произведения по каждому его сомножителю
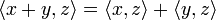 ,
,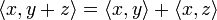 ,
,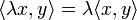 ,
,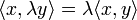 ,
,
- где
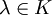 .
.
- где
2 - аксиома эрмитовости внутреннего произведения
Здесь через
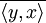 обозначено число, комплексно сопряжённое к
обозначено число, комплексно сопряжённое к 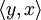
3 - Чаще всего рассматривается случай, когда скалярное произведение является положительно определённым, то есть к аксиомам линейности добавляется
аксиома положительной определённости: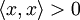 для любого
для любого 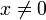 ,
,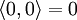 .
.
В этом случае на пространстве L можно ввести порождённую внутренним произведением норму вида
удовлетворяющую неравенству Коши — Буняковского, а значит, оснащённое таким внутренним произведением пространство является также метрическим и топологическим.
Скалярное произведение
Скалярное произведение (англ. scalar product, dot product) является частным случаем внутреннего произведения (англ. inner product). Скалярное произведение может быть введено только в действительном векторном пространстве. А так называемое внутренное произведение вводится в комплексном векторном пространстве. В советских книгах понятие внутреннего произведения не вводилось, поэтому и то и другое называлось скалярным произведением.
Примечания
- ↑ Векторное пространство, о котором идет речь, может, например, быть конечномерным либо бесконечномерным, и это сказывается на терминологии: как именно принято называть такое пространство, снабженное внутренним произведением. Например, термин 'предгильбертово (гильбертово)' пространство применим к бесконечномерным пространствам, а 'евклидово' — лишь к конечномерным.
- ↑ Когда говорят о внутреннем произведении, практически всегда выполняются аксиомы линейности (исключений из этого правила, пожалуй, нет), но остальные аксиомы (эрмитовости/симметричности и положительной определенности) могут выполняться для одного типа внутреннего произведения и не выполняться для другого (хотя по умолчанию обычно подразумеваются выполняющимися все); и эта разница типа (основного) внутреннего произведения, определенного на данном пространстве, влияет на принятое для соответствующего пространства название. Так, конечномерное векторное пространство с положительно определенным внутренним произведением называется евклидовым, а пространство с индефинитным внутренним произведением, которое для некоторых x дает
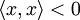 — псевдоевклидовым.
— псевдоевклидовым.
Wikimedia Foundation. 2010.