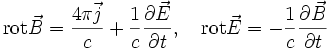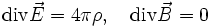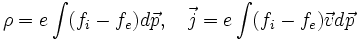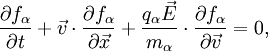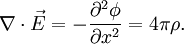Власова — Пуассона приближение

Уравнение Власова — система уравнений, описывающих динамику плазмы заряженных частиц с учетом дальнодействующих кулоновских сил посредством самосогласованного поля. Впервые предложена А. А. Власовым в статье^[1] и позднее излагается в монографии^[2].

Проблемы газокинетического подхода

В своей работе Власов сначала указывает на неприменимость газокинетического подхода, основанного на уравнении Больцмана, к описанию динамики плазмы с кулоновским взаимодействием. Он отмечает следующие проблемы, возникающие при попытке применения теории парных столкновений к описанию плазмы:

1. Теория парных столкновений не согласуется с исследованиями Рэлея и Ленгмюра и Тонкса о наличии собственных вибраций в электронной газовой плазме.
2. Теория парных столкновений формально не применима к кулоновскому взаимодействию из-за расходимости кинетических членов.
3. Теория парных столкновений не позволяет объяснить эксперименты Меррилла и Вебба об аномальном рассеянии электронов в газовой плазме.

В качестве причины возникновения этих проблем Власов указывает на дальнодействующий характер кулоновских сил.

Уравнения Власова — Максвелла

Затем, вместо описания взаимодействия заряженных частиц в плазме посредством столкновений, предлагается использовать самосогласованное поле, созданное заряженными частицами плазмы. Для этого описания вводятся функции распределения 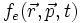$f_e(\vec{r},\vec{p},t)$ электронов и 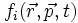$f_i(\vec{r},\vec{p},t)$ (положительных) ионов плазмы. Вместо уравнения Больцмана Власов предлагает использовать следующую систему уравнений для описания заряженных компонент плазмы (электронов и положительных ионов):

$\frac{\partial f_e}{\partial t} + \vec{v} \frac{\partial f_e}{\partial\vec{x}} - e\Bigl(\vec{E}+\frac{1}{c}[\vec{v},\vec{B}]\Bigr) \frac{\partial f_e}{\partial\vec{p}} = 0$

$\frac{\partial f_i}{\partial t} + \vec{v} \frac{\partial f_i}{\partial \vec{x}} + e\Bigl(\vec{E}+\frac{1}{c}[\vec{v},\vec{B}]\Bigr) \frac{\partial f_i}{\partial \vec{p}} = 0$

${\rm rot}\vec{B}=\frac{4\pi\vec{j}}{c}+\frac{1}{c}\frac{\partial\vec{E}}{\partial t},\quad {\rm rot}\vec{E}=-\frac{1}{c}\frac{\partial\vec{B}}{\partial t}$

${\rm div}\vec{E}=4\pi\rho,\quad {\rm div}\vec{B}=0$

$\rho=e\int(f_i-f_e)d\vec{p},\quad \vec{j}=e\int(f_i-f_e)\vec{v}d\vec{p}$

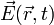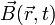Здесь e — заряд электрона, c — скорость света, $\vec{E}(\vec{r},t)$ и $\vec{B}(\vec{r},t)$ — самосогласованное электрическое и магнитное поле, созданное в точке 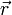$\vec{r}$ в момент времени t всеми заряженными частицами плазмы. Существенное отличие этой системы уравнений от уравнений движения заряженных частиц во внешнем электромагнитном поле в том, что само самосогласованное электромагнитное поле сложным образом зависит от функций распределения ионов и электронов.

Уравнения Власова — Пуассона

Уравнения Власова — Максвелла являются системой нелинейных интегро-дифференциальных уравнений. Если флуктуации функций распределения относительно равновесного состояния невелики, эта система уравнений может быть линеаризована. Линеаризация даст систему уравнений Власова — Пуассона, описывающую динамику плазмы в самосогласованном электрическом поле. Уравнения Власова — Пуассона являются системой уравнений Власова для каждой компоненты плазмы (рассматриваем нерелятивистский предел):

$\frac{\partial f_{\alpha}}{\partial t} + \vec{v} \cdot \frac{\partial f_{\alpha}}{\partial \vec{x}} + \frac{q_{\alpha}\vec{E}}{m_{\alpha}} \cdot \frac{\partial f_{\alpha}}{\partial \vec{v}} = 0,$

и уравнения Пуассона для самосогласованного электрического поля:

$\nabla \cdot \vec{E} = -\frac{\partial^2\phi}{\partial x^2} = 4 \pi \rho.$

Здесь q_α — электрический заряд и m_α — масса частиц плазмы, 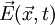$\vec{E}(\vec{x},t)$ — самосогласованное электрическое поле, 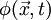$\phi(\vec{x}, t)$ — потенциал самосогласованного электрического поля и ρ — плотность электрического заряда.

Примечания

1. ↑ А. А. Власов. О вибрационных свойствах электронного газа // Журнал экспериментальной и теоретической физики. — 1938. — Т. 8 (3). — С. 291.
2. ↑ А. А. Власов. Теория вибрационных свойств электронного газа и ее приложения // Уч. зап. МГУ. — 1945. — В. 75. Кн. 2. Ч. 1.

Литература

• И. П. Базаров, П. Н. Николаев. Анатолий Александрович Власов. — Физический факультет МГУ. — М.: 1999. — С. 19—26. — (Выдающиеся учёные физического факультета МГУ). — Подробное обсуждение уравнений Власова.