Частные производные высших порядков.

Пусть задана функция f(x, y). Тогда каждая из ее частных производных(если они, конечно, существуют) $\partial f(x,y)\over\partial x$ и $\partial f(x,y)\over\partial y$, которые называются также частными производными первого порядка, снова являются функцией независимых переменных x, y и может, следовательно также иметь частные производные. Частная производная ${\partial \over {\partial x}} ({\partial f\over{\partial x}})$ обозначается через ${\partial^2 f \over {\partial x^2}}$ или f_xx, а ${\partial\over {\partial y}} ({\partial f \over {\partial x }})$ через $\partial^2 f\over{\partial y\partial x}$ или f_xy. Таким образом,

${\partial\over{\partial x}} ({\partial f \over{\partial x}})={\partial^2 f\over{\partial x^2}}=f_{xx}$,${\partial\over{\partial x}} ({\partial f \over{\partial x}})={\partial^2 f\over{\partial y\partial x}}=f_{xy}$

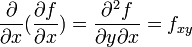
и,аналогично,

${\partial\over{\partial x}} ({\partial f \over{\partial y}})={\partial^2 f\over{\partial x\partial y}}=f_{yx}$, ${\partial\over{\partial y}} ({\partial f \over{\partial x}})={\partial^2 f\over{\partial y^2}}=f_{yy}$.

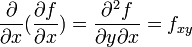
Производные f_xx, f_xy, f_yx и f_yy называются частными производными второго порядка. Рассматривая частные производные от них, получим всевозможные частные производные третьего порядка: $\partial^3 f\over{\partial x^3}$, $\partial^3 f\over{\partial y\partial x^2}$, $\partial^3 f\over{\partial y^2\partial x}$ и т.д.