- дифференциальное исчисление
- дифференциа́льное исчисле́ниераздел математики, в котором изучаются производные, дифференциалы и их применения к исследованию свойств функций. Производной функции у = f(х) называется предел отношения приращения Δу = у1 – у0 функции к приращению Δх = x1 – х0 аргумента при Δх, стремящемся к нулю (если этот предел существует). Производная обозначается f\'(х) или у\'; т.о.,
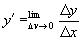 . Дифференциалом функции у = f(х) называется выражение dy = у´dx, где dx = Δх — приращение аргумента х. Очевидно, что у\' = dy/dx. Отношение dy/dx часто употребляют как знак производной. Вычисление производных и дифференциалов называют дифференцированием. Если производная f\'(х) имеет, в свою очередь, производную, то её называют второй производной функции f(x) и обозначают f"(х), и т. д. Основные понятия дифференциального исчисления могут быть распространены на случай функций нескольких переменных. Если z = f(х, у) — функция двух переменных х и у, то, зафиксировав для у какое-либо значение, можно дифференцировать z по х; полученная производная
. Дифференциалом функции у = f(х) называется выражение dy = у´dx, где dx = Δх — приращение аргумента х. Очевидно, что у\' = dy/dx. Отношение dy/dx часто употребляют как знак производной. Вычисление производных и дифференциалов называют дифференцированием. Если производная f\'(х) имеет, в свою очередь, производную, то её называют второй производной функции f(x) и обозначают f"(х), и т. д. Основные понятия дифференциального исчисления могут быть распространены на случай функций нескольких переменных. Если z = f(х, у) — функция двух переменных х и у, то, зафиксировав для у какое-либо значение, можно дифференцировать z по х; полученная производная 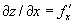 называется частной производной z по х. Аналогично определяются частная производная
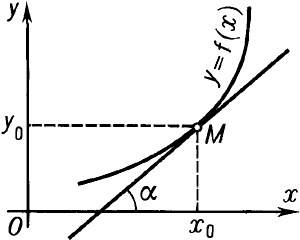
называется частной производной z по х. Аналогично определяются частная производная  , частные производные высших порядков, частные и полные дифференциалы. Для приложений дифференциального исчисления к геометрии важно, что так называемый угловой коэффициент касательной, то есть тангенс угла α (см. рис.) между осью Ох и касательной к кривой у = f(х) в точке М(х0, у0), равен значению производной при х = х0, то есть f\'(х0). В механике скорость прямолинейно движущейся точки можно истолковать как производную пути по времени. Дифференциальное исчисление (как и интегральное исчисление) имеет многочисленные применения.
, частные производные высших порядков, частные и полные дифференциалы. Для приложений дифференциального исчисления к геометрии важно, что так называемый угловой коэффициент касательной, то есть тангенс угла α (см. рис.) между осью Ох и касательной к кривой у = f(х) в точке М(х0, у0), равен значению производной при х = х0, то есть f\'(х0). В механике скорость прямолинейно движущейся точки можно истолковать как производную пути по времени. Дифференциальное исчисление (как и интегральное исчисление) имеет многочисленные применения.
 * * *ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕДИФФЕРЕНЦИА́ЛЬНОЕ ИСЧИСЛЕ́НИЕ, раздел математики, в котором изучаются производные, дифференциалы и их применения к исследованию свойств функций.
* * *ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕДИФФЕРЕНЦИА́ЛЬНОЕ ИСЧИСЛЕ́НИЕ, раздел математики, в котором изучаются производные, дифференциалы и их применения к исследованию свойств функций.
Производной функции y = f(х) называется предел отношения приращения Dy = y1 — y0 функции к приращению Dx = x1 – x0 аргумента при Dx, стремящемся к нулю (если этот предел существует). Дифференциалом функции y = f(x) называется выражение dy = yўdx, где dx = Dx — приращение аргумента x. Очевидно, что yў = dy/dx. Отношение dy/dx часто употребляют как знак производной. Вычисление производных и дифференциалов называют дифференцированием. Если производная fў(x) имеет, в свою очередь, производную, то ее называют 2-й производной функции f(x) и обозначают fўў(x), и т. д. Основные понятия дифференциального исчисления могут быть распространены на случай функций нескольких переменных. Если z = f(x,y) — функция двух переменных x и y, то, зафиксировав для y какое-либо значение, можно дифференцировать z по x; полученная производная dz/dx = fўx называется частной производной z по x. Аналогично определяются частная производная dz/dy = fўy, частные производные высших порядков, частные и полные дифференциалы.
Для приложений дифференциального исчисления к геометрии важно, что т. н. угловой коэффициент касательной, т. е. тангенс угла a между осью Ox и касательной к кривой y = f(x) в точке M(x0, y0), равен значению производной при x = x0, т. е. fў(x0). В механике скорость прямолинейно движущейся точки можно истолковать как производную пути по времени. Дифференциальное исчисление (как и интегральное исчисление (см. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ)) имеет многочисленные применения.
Энциклопедический словарь. 2009.
