Задача трехмерной упаковки в объем

В теории сложности вычислений задача об упаковке в контейнеры — NP-трудная комбинаторная задача. Задача заключается в упаковке объектов предопределённой формы в конечное число контейнеров предопределённой формы таким способом, чтобы число использованных контейнеров было наименьшим или количество или объём объектов (которые упаковывают) были наибольшими.

Существует множество разновидностей этой задачи (двумерная упаковка, линейная упаковка, упаковка по весу, упаковка по стоимости и т.п.), которые могут применяться в разных областях, как собственно в вопросе оптимального заполнения контейнеров, загрузки грузовиков с ограничением по весу, созданием резервных копий на съёмных носителях и т.д.

Так как задача является NP-трудной зачастую используют алгоритмы с эвристическим и метаэвристическим методом решения для получения оптимальных результатов. Так же активно используются методы искусственного интеллекта, как, например, нейронные сети.

Стратегии Best Fit Decreasing и First Fit Decreasing используют не более 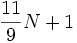$\frac{11}{9}N + 1$ контейнеров (где N - число контейнеров при наилучшем решении задачи). Однако, существуют алгоритмы приближения, которые могут решить задачу об упаковке с любым наперёд заданным процентом наилучшего решения для больших массивов исходных данных (они называются асимптотической схемой приближения полиномиального времени). Всё это выделяет задачу среди большинства других основных NP-трудных задач, некоторые из которых не могут быть приближены вообще.

Примечания

См. также

• Задача упаковки
• Задача о ранце
• Задача о сумме подмножеств
• Оптимизация
• Упаковка шаров

Ссылки