- Периодограмма
-
Периодограмма — оценка спектральной плотности мощности (СПМ), основанная на вычислении квадрата модуля преобразования Фурье последовательности данных с использованием статистического усреднения:
![S_T(\omega)=E\left[\frac{|X_T(i\omega)|^2}{T_r}\right]](7dd3368b5a90b26c1172b04cafe5a5ad.png)
 — преобразование Фурье функции
— преобразование Фурье функции  на конечном временном интервале,
на конечном временном интервале,  — интервал финитности,
— интервал финитности,  — оператор статистического усреднения (математическое ожидание). Если при расчёте СПМ используется весовая функция (окно), то полученная оценка СПМ называется модифицированной периодограммой. Периодограмма не является состоятельной оценкой СПМ, поскольку дисперсия такой оценки сравнима с квадратом её математического ожидания. С ростом числа используемых отсчётов значения периодограммы начинают всё быстрее флуктуировать.
— оператор статистического усреднения (математическое ожидание). Если при расчёте СПМ используется весовая функция (окно), то полученная оценка СПМ называется модифицированной периодограммой. Периодограмма не является состоятельной оценкой СПМ, поскольку дисперсия такой оценки сравнима с квадратом её математического ожидания. С ростом числа используемых отсчётов значения периодограммы начинают всё быстрее флуктуировать.
Содержание
Исторические сведения
- Термин периодограмма впервые был упомянут Артуром Шустером в 1898[1] году. Шустер применил периодограмму для отыскания периодичностей в записях метеорологических наблюдений, записях магнитного склонения и ряда чисел солнечных пятен. Он выполнил предварительную обработку среднемесячных значений числа солнечных пятен за период с 1749 по 1894 год. Периодограммный анализ позволил дать оценку цикла солнечных пятен, равную 11,125 года. Шустер указал многочисленные трудности, связанные с вычислением периодограммы, и характерные её особенности. Изменяя начало отсчёта времени, он получал образцы периодограммы с различными нерегулярными изменениями, причём эти периодограммы иногда содержали ложные пики (Шустер называл их «случайными периодичностями») там, где в действительности никакой периодичности не существовало. Шустер из своего опыта гармонического анализа оптических спектров знал, что усреднение значений, полученных для различных отрезков последовательности данных необходимо для сглаживания периодограммы (получения «средней периодограммы» в его терминологии) и устранения ложных пиков. И хотя Шустер установил необходимость усреднения, практическая его реализация требовала вычислительных средств, далеко выходящих за рамки имеющихся в те годы технических возможностей. Шустер также понимал, что боковые лепестки (которые он называл «ложными периодичностями») вокруг главных лепестков в периодограмме являются неотъемлемой особенностью любого метода анализа Фурье записей данных конечной длины.
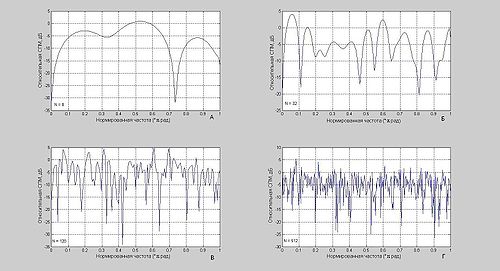
- Многие исследователи начала прошлого столетия считали, что периодограммы, вычисленные по зашумлённым данным, будут иметь значительные погрешности и вообще не будут содержать каких-либо доминирующих пиков, которые могли бы свидетельствовать о наличии периодичностей в анализируемых данных. Причём это считалось справедливым даже тогда, когда длина записи данных существенно возрастала. Примеры таких периодограмм показаны на рисунке, из которого видно, что с использованием всё большего и большего числа отсчётов данных периодограмма начинает всё сильнее и сильнее флуктуировать. Всё это привело к тому, что на несколько десятилетий интерес к периодограммам значительно ослабел, и это в основном можно объяснить лишь тем, что большинство исследователей пренебрегало усреднением, использовать которое предлагал Шустер. Слуцкий и несколько позднее Даньелл независимо установили, что флуктуации периодограммы белого шума имеют ту же величину, что и среднее значение самой этой периодограммы. Эти флуктуации оказывались в основном некоррелированными для соседних частот. Слуцкий и Даньелл высказали предположение, что флуктуации периодограммы можно уменьшить посредством её усреднения по соседним частотам. Эта идея лежит в основе одного из методов сглаживания периодограммы.
См. также
Литература
- Марпл-мл. С. Л. Цифровой спектральный анализ и его приложения. — М.: МИР, 1990. — С. 584.
- Айфичер Э., Джервис Б. Цифровая обработка сигналов: практический подход. — 2-е. — М.: Вильямс, 2004. — С. 992. — ISBN 5-8459-0710-1 (рус.)
- Шахтарин Б. И., Ковригин В. А. Методы спектрального оценивания случайных процессов. — М.: Гелиос АРВ, 2005. — С. 248. — ISBN 5-85438-136-2
- Сергиенко А. Б. Цифровая обработка сигналов. — 2-е. — Спб: Питер, 2006. — С. 751. — ISBN 5-469-00816-9
Ссылки
- ↑ Schuster, A., "On the investigation of hidden periodicities with application to a supposed 26 day period of meteorological phenomena, " Terrestrial Magnetism and Atmospheric Electricity, 3, 13-41, 1898.

Эту статью следует викифицировать. Пожалуйста, оформите её согласно правилам оформления статей.Категория:- Обработка сигналов
Wikimedia Foundation. 2010.