- ПЕРИОДОГРАММА
- функция IN(l).
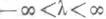 N - целое положительное, определяемая по выборке Х(1), . . ., X(N).стационарного случайного процесса X(t), t=0, +1, . . ., следующим образом:
N - целое положительное, определяемая по выборке Х(1), . . ., X(N).стационарного случайного процесса X(t), t=0, +1, . . ., следующим образом:

где

П. является периодической по l, функцией с периодом 2p. Дифференцируемая спектральная плотность f(l).стационарного процесса X(t).со средним
 может быть оценена с помощью П. при
может быть оценена с помощью П. при 
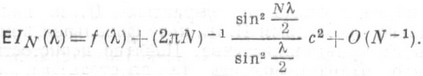
В то же время П. не является состоятельной оценкой f(l) (см. [1]). Состоятельные спектральной плотности оценки могут быть получены на основе нек-рых дальнейших построений, использующих асимптотическую некоррелированность П. разных частот
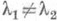 , так что осреднение IN (х).по близким к l частотам может привести к асимптотически состоятельной оценке. В случае n-мерного случайного процесса
, так что осреднение IN (х).по близким к l частотам может привести к асимптотически состоятельной оценке. В случае n-мерного случайного процесса  матрица периодограммы IN(l) определяется своими элементами
матрица периодограммы IN(l) определяется своими элементами
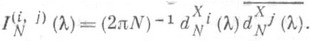
Наряду с периодограммой IN(l), к-рую еще наз. П. 2-го порядка, иногда рассматривают П. m-го порядка

к-рые используют для построения оценок спектральных плотностей m-го порядка (см. Спектральный семиинвариант).
Лит.:[1] Бриллинджер Д., Временные ряды. Обработка данных и теория, пер. с англ., М., 1980; [2] Xеннан Э., Многомерные временные ряды, пер. с англ., М., 1974. .
И. Г. Журбенко.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
