Правило умножения (комбинаторика)

Правило умножения (комбинаторика)

Правило умножения (комбинаторика)

Правило умножения, иначе называемое правилом «и» — одно из основных правил комбинаторики. Согласно ему, если элемент A можно выбрать n способами и, при любом выборе A (то есть независимо), элемент B можно выбрать m способами, то пару (A, B) можно выбрать n*m способами. Естественным образом обобщается на произвольную длину последовательности.

Ключевые выражения в формулировке, приводящие к правилу умножения: «и то, и другое», «одновременно», «независимо», «каждый из».

Содержание

Примеры

Простой

Выбрать книгу и диск из 10 книг и 12 дисков можно 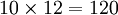10\times 12=120 способами. Правило сложения

Количество размещений с повторениями

Если есть множество из n типов элементов и нужно на каждое из m мест расположить элемент какого-либо типа (типы элементов могут совпадать на разных местах), то количество вариантов этого будет nm, так как выборы независимы.

Составной

Пусть требуется найти количество слов, составленных не более, чем из 3 букв алфавита {a, b,c, d}. Количество n-буквенных слов равно количеству размещений из 4 букв на n мест с повторениями — оно равно 4n. Количество всех слов (так как нужно учитывать любое из слов) будет складываться из количеств одно-, двух- и трёхбуквенных слов. Тогда ответ на первоначальный вопрос будет 41 + 42 + 43 = 84.


Wikimedia Foundation. 2010.

Игры ⚽ Поможем сделать НИР

Полезное


Смотреть что такое "Правило умножения (комбинаторика)" в других словарях:

  • Правило сложения (комбинаторика) — Правило сложения (правило «или») одно из основных правил комбинаторики, утверждающее, что, если элемент A можно выбрать n способами, а элемент B можно выбрать m способами, то выбрать A или B можно n + m способами. Содержание 1 Примеры 1.1 Пример… …   Википедия

  • Правило умножения — (правило «и»)  одно из основных правил комбинаторики. Согласно ему, если элемент A можно выбрать n способами, и при любом выборе A элемент B можно выбрать m способами, то пару (A, B) можно выбрать n·m способами. Естественным образом… …   Википедия

  • История арифметики — Арифметика. Роспись Пинтуриккьо. Апартаменты Борджиа. 1492 1495. Рим, Ватиканские дворцы …   Википедия

  • Арифметика — Ганс Себальд Бехам. Арифметика. XVI век Арифметика (др. греч. ἀ …   Википедия

  • Дифференциальная алгебра — Дифференциальными кольцами, полями и алгебрами называются кольца, поля и алгебры, снабжённые дифференцированием  унарной операцией, удовлетворяющей правилу произведения. Естественный пример дифференциального поля  поле рациональных… …   Википедия

  • Математика в Древнем Египте — Данная статья  часть обзора История математики. Статья посвящена состоянию и развитию математики в Древнем Египте в период примерно с XXX по III век до н. э. Древнейшие древнеегипетские математические тексты относятся к началу II… …   Википедия

  • Вавилонская математика — Данная статья часть обзора История математики. Вавилонская табличка с вычислением = 1.41421296... Вавилоняне писали …   Википедия

  • Прямое произведение — Прямое или декартово произведение  множество, элементами которого являются всевозможные упорядоченные пары элементов исходных двух множеств. Данное понятие употребляется не только в теории множеств, но также в алгебре, топологии и прочих… …   Википедия

  • Декартова степень — Прямое или декартово произведение множеств  множество, элементами которого являются всевозможные упорядоченные пары элементов исходных двух множеств. Данное понятие употребляется не только в теории множеств, но также в алгебре, топологии и прочих …   Википедия

  • Декартово произведение — Прямое или декартово произведение множеств  множество, элементами которого являются всевозможные упорядоченные пары элементов исходных двух множеств. Данное понятие употребляется не только в теории множеств, но также в алгебре, топологии и прочих …   Википедия


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»