SEAL (криптографический алгоритм)

Схема алгоритма SEAL

У этого термина существуют и другие значения, см. SEAL (значения).

SEAL (англ. Software-optimized Encryption Algorithm, программно-оптимизированный алгоритм шифрования) — симметричный поточный алгоритм шифрования данных, оптимизированный для программной реализации.

Разработан в IBM Филом Рогэвеем (англ.) (англ. Phil Rogaway) и Доном Копперсмитом (англ. Don Coppersmith) в 1993 году. Алгоритм оптимизирован и рекомендован для 32-битных процессоров. Для работы ему требуется кэш-память на несколько килобайт и восемь 32-битовых регистров. Cкорость шифрования — примерно 4 машинных такта на байт текста. Для кодирования и декодирования используется 160-битный ключ. Чтобы избежать нежелательной потери скорости по причине медленных операций обработки ключа, SEAL предварительно выполняет с ним несколько преобразований, получая в результате три таблицы определенного размера. Непосредственно для шифрования и расшифрования текста вместо самого ключа используются эти таблицы.

Алгоритм считается очень надёжным, очень быстрым^[1] и защищён патентом США № 5454039^[2] с декабря 1993 года.

История

В 1991 году Ральф Меркл (англ. Ralph C. Merkle) описал рентабельность программно-ориентированных шифров. По его мнению, наиболее эффективными из них были Khufu, FEAL и RC4. Однако постоянно увеличивающиеся потребности клиентов в надежной криптографии требовали поиска новых и доработки старых решений.

Летом 1992 года началась разработка первой версии нового программно-оптимизированного алгоритма SEAL 1.0. Разработчики взяли основные идеи и принцип работы из блочного шифра Ральфа Меркла (англ. Ralph C. Merkle) Khufu, который показался им самым совершенным на тот момент. Они решили добиться лучших характеристик проекта (в основном скорости), сузив круг аппаратуры, на которой возможна его реализация. Выбор был сделан в пользу 32-битных машин минимум с восемью регистрами общего назначения и кэшем не менее 8 Кбайт. В марте 1993 года было принято решение создать блочный шифр, но структура из семейства псевдослучайных функций, разработанная к октябрю того же года, работала быстрее, что склонило разработчиков в к поточному шифрованию. Эта структура состояла из четырех регистров, каждый из которых изменял своего «соседа» в зависимости от таблицы, полученной из ключа. После некоторого количества таких модификаций значения регистров добавляются в ключевую последовательность, которая растет с каждой итерацией до тех пор, пока не достигнет определенной длины. При разработке почти все внимание уделялось внутреннему циклу алгоритма, так как процедуру инициализации регистров и метод генерации таблиц из ключа оказывали незначительное влияние на его защищенность. В окончательном виде проект SEAL 1.0 появился только в декабре 1993 года.

В 1996 году Helena Handschuh (англ.) и Henri Gilbert (англ.) описали атаки на упрощенную версию SEAL 1.0 и на сам SEAL 1.0. Им потребовалось $2^{30}$ текстов, каждый длиной в четыре 32-битных слова, чтобы найти зависимость псевдослучайной функции от ключа. В результате, в следующих версиях алгоритма SEAL 3.0 и SEAL 2.0 были сделаны некоторые доработки и изменения. Например, в версии 1.0 каждая итерация с ключевой последовательностью завершалась модификацией только двух регистров, а в версии 3.0 — модифицировались все четыре. Еще SEAL 3.0 и SEAL 2.0 использовали для генерации таблиц алгоритм SHA-1 (англ. Secure Hash Algorithm-1) вместо первоначального SHA, что сделало их более устойчивыми к криптоанализу.

Описание

При описании алгоритма используются следующие операции и обозначения:

• числа шестнадцатеричной системы счисления начинаются с символов «0x» и используют в записи кроме десятичных цифр символы «a», «b», «c», «d», «e» и «f», которые обозначают десятичные числа от 10 до 15 соответственно;
• под выражением Y $\ggg$ t следует понимать циклический сдвиг регистра Y вправо на t бит;
• под выражением Y $\lll$ t следует понимать циклический сдвиг регистра Y влево на t бит;
• операция X $\And$ Y означает побитовое логическое умножение (англ. AND) регистров X и Y;
• операция X $\lor$ Y означает побитовое логическое сложение (англ. OR) регистров X и Y;
• операция X $\oplus$ Y означает побитовое сложение по модулю 2 (англ. XOR) регистров X и Y;
• под X $\lVert$ Y следует понимать конкатенацию (англ. Concatenation) регистров X и Y;
• выражение odd (X) обозначает логическую функцию аргумента X, которая принимает значение ИСТИНА (англ. TRUE) только, если X — чётное число.

Создание таблиц шифрования из ключа

Чтобы избежать потери скорости шифрования на медленных операциях алгоритм использует три таблицы: R, S и T. Эти таблицы вычисляются с помощью процедуры из алгоритма SHA-1 и зависят только от ключа. Заполнение данных таблиц можно описать с помощью функции G, которая из 160-битной строки $~a$ и 32-битного числа $~i$ возвращает 160-битное значение $~G_a(i)$.

Введем следующие функции и переменные в зависимости от индекса $~t$:

• для $0 \le t \le 19$ установим $~K_t = \mbox{0x}5a827999$ и $f_t (B, C, D) = (B \And C) \lor (B \And D);$
• для $20 \le t \le 39$ установим $~K_t = \mbox{0x}6ed9eba1$ и $f_t (B, C, D) = B \oplus C \oplus D;$
• для $40 \le t \le 59$ установим $~K_t = \mbox{0x}8f1bbcdc$ и $f_t (B, C, D) = (B \And C) \lor (B \And D) \lor (C \And D);$
• для $60 \le t \le 79$ установим $~K_t = \mbox{0x}ca62c1d6$ и $f_t (B, C, D) = B \oplus C \oplus D.$

Затем 160-битную строка $~a$ разбивается на пять 32-битных слов так, что $~a = H_0 \lVert H_1 \lVert H_2 \lVert H_3 \lVert H_4.$

Также создается шестнадцать 32-битных слов $~W_0 = i,~~W_1 = W_2 =...= W_{15} = 0^{32}.$

Затем выполняются финальные вычисления:

1. $\mbox{For}~t = 16~\mbox{to}~79~\mbox{do}~W_t = (W_{t-3} \oplus W_{t-8} \oplus W_{t-14} \oplus W_{t-16}) \lll 1;$
2. $A = H_0;~B = H_1;~C = H_2;~D = H_3;~E = H_4;$
3. $\mbox{For}~t = 0~\mbox{to}~79~\mbox{do}$

   $\mbox{TEMP} = A \lll 5 + f_t(B, C, D) + E + W_t + K_t;$

   $E = D;~D = C;~C = B \lll 30;~B = A;~A = TEMP;$

4. $H_0 = H_0 + A;~H_1 = H_1 + B;~H_2 = H_2 + C;~H_3 = H_3 + D; H_4 = H_4 + E;$
5. $~G_a(i) = H_0 \lVert H_1 \lVert H_2 \lVert H_3 \lVert H_4.$

Введем функцию $~\Gamma_a(i) = H^i_{i~mod~5}$ где $H_0^{5j} \lVert H_1^{5j+1} \lVert H_2^{5j+2} \lVert H_3^{5j+3} \lVert H_4^{5j+4} = G_a(j)$ для $~j = \mathcal {b} i/5 \mathcal {c}.$

Тогда таблицы:

$~T[i] = \Gamma_a(i),~~0 \le i < 512;$

$~S[j] = \Gamma_a(\mbox{0x}1000 + j),~~0 \le j < 256;$

$~R[k] = \Gamma_a(\mbox{0x}2000 + k),~~0 \le k < 256.$

Далее ключ $~a$ в алгоритме не используется.

Инициализация служебных регистров

Перед генерацией псевдослучайной функции нужно подготовить четыре 32-битовых служебных регистра ($A$, $B$, $C$ и $D$) и четыре 32-битовых слова ($n_1$, $n_2$, $n_3$ и $n_4$). Их значения определяются из таблиц $R$ и $T$, 32-битового числа $n$ и некоторого числа $l$ в следующей процедуре.

$\mbox{procedure}~\mbox{Initialize}~(n, l, A, B, C, D, n_1, n_2, n_3, n_4)$

$A \leftarrow n \oplus R[4l];$

$B \leftarrow (n \ggg 8) \oplus R[4l + 1];$

$C \leftarrow (n \ggg 16) \oplus R[4l + 2];$

$D \leftarrow (n \ggg 24) \oplus R[4l + 3];$

$\mbox{for}~j \leftarrow 1~\mbox{to}~2~\mbox{do}$

$P \leftarrow A \And \mbox{0x}7fc;~~B \leftarrow B + T[P/4];~~A \leftarrow A \ggg 9;$

$P \leftarrow B \And \mbox{0x}7fc;~~C \leftarrow C + T[P/4];~~B \leftarrow B \ggg 9;$

$P \leftarrow C \And \mbox{0x}7fc;~~D \leftarrow D + T[P/4];~~C \leftarrow C \ggg 9;$

$P \leftarrow D \And \mbox{0x}7fc;~~A \leftarrow A + T[P/4];~~D \leftarrow D \ggg 9;$

$(n_1, n_2, n_3, n_4) \leftarrow (D, B, A, C);$

$P \leftarrow A \And \mbox{0x}7fc;~~B \leftarrow B + T[P/4];~~A \leftarrow A \ggg 9;$

$P \leftarrow B \And \mbox{0x}7fc;~~C \leftarrow C + T[P/4];~~B \leftarrow B \ggg 9;$

$P \leftarrow C \And \mbox{0x}7fc;~~D \leftarrow D + T[P/4];~~C \leftarrow C \ggg 9;$

$P \leftarrow D \And \mbox{0x}7fc;~~A \leftarrow A + T[P/4];~~D \leftarrow D \ggg 9;$

Создание псевдослучайной функции

Для шифрования текста необходимо создать псевдослучайную функцию.

$\mbox{function}~\mbox{SEAL}~(a, n, L)$

$~y = 0^L;$

$\mbox{for}~l \leftarrow 0~\mbox{to}~\infty~\mbox{do}$

      $\mbox{Initialize}~(n, l, A, B, C, D, n_1, n_2, n_3, n_4);$

      $\mbox{for}~i \leftarrow 1~\mbox{to}~64~\mbox{do}$

            $P \leftarrow A \And \mbox{0x}7fc;~~B \leftarrow B + T[P/4];~~A \leftarrow A \ggg 9;~~B \leftarrow B \oplus A;$

            $Q \leftarrow B \And \mbox{0x}7fc;~~C \leftarrow C \oplus T[Q/4];~~B \leftarrow B \ggg 9;~~C \leftarrow C + B;$

            $P \leftarrow (P + C) \And \mbox{0x}7fc;~~D \leftarrow D + T[P/4];~~C \leftarrow C \ggg 9;~~D \leftarrow D \oplus C;$

            $Q \leftarrow (Q + D) \And \mbox{0x}7fc;~~A \leftarrow A \oplus T[Q/4];~~D \leftarrow D \ggg 9;~~A \leftarrow A + D;$

            $P \leftarrow (P + A) \And \mbox{0x}7fc;~~B \leftarrow B \oplus T[P/4];~~A \leftarrow A \ggg 9;$

            $Q \leftarrow (Q + B) \And \mbox{0x}7fc;~~C \leftarrow C + T[Q/4];~~B \leftarrow B \ggg 9;$

            $P \leftarrow (P + C) \And \mbox{0x}7fc;~~D \leftarrow D \oplus T[P/4];~~C \leftarrow C \ggg 9;$

            $Q \leftarrow (Q + D) \And \mbox{0x}7fc;~~A \leftarrow A + T[Q/4];~~D \leftarrow D \ggg 9;$

            $y \leftarrow y~\lVert~B + S[4i-4]~\lVert~C \oplus S[4i-3]~\lVert~D + S[4i-2]~\lVert~A \oplus S[4i-1];$

            $\mbox{if}~|y| \ge L~\mbox{then}~\mbox{return}~~y_0y_1...y_{L-1};$

            $\mbox{if}~odd(i)~\mbox{then}~(A, B, C, D) \leftarrow (A + n_1, B + n_2, C \oplus n_1, D \oplus n_2);$

                                $\mbox{else}~(A, B, C, D) \leftarrow (A + n_3, B + n_4, C \oplus n_3, D \oplus n_4);$

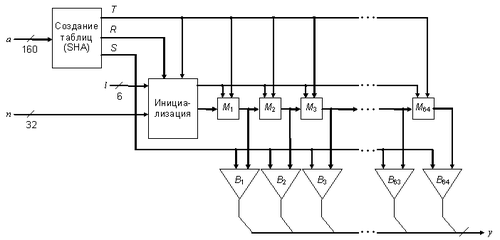
Процесс шифрования состоит из большого числа итераций, каждая из которых завершается генерацией псевдослучайной функции. Количество пройденных итераций показывает счетчик l. Все они подразделяются на несколько этапов с похожими операциями. На каждом этапе старшие 9 битов одного из регистров (A, B, C или D) используются в качестве указателя, по которому из таблицы T выбирается значение. Это значение складывается арифметически или поразрядно по модулю 2 (XOR) со следующим регистром (снова один из A, B, C или D). Затем первый выбранный регистр преобразуется циклическим сдвигом вправо на 9 позиций. Далее либо значение второго регистра модифицируется сложением или XORом с содержимым первого (уже сдвинутым) и выполняется переход к следующему этапу, либо этот переход выполняется сразу. После 8 таких этапов значения A, B, C и D складываются (арифметически или XORом) с определенными словами из таблицы S и добавляются в ключевую последовательность y. Завершающий этап итерации заключается в прибавлении к регистрам дополнительных 32-битных значений (n1, n2 или n3, n4). Причем выбор конкретного значения зависит от четности номера данной итерации.

Свойства и практическое применение

При разработке этого алгоритма главное внимание отводилось следующим свойствам и идеям:

• использование большой (примерно 2 Kбайта) таблицы T, получаемой из большого 160-битного ключа;
• чередование арифметических операций (сложение и побитовый XOR);
• использование внутреннего состояния системы, которое явно не проявляется в потоке данных (значения n1, n2, n3 и n4, которые изменяют регистры в конце каждой итерации);
• использование отличных друг от друга операций в зависимости от этапа итерации и ее номера.

Для шифрования и расшифрования каждого байта текста шифр SEAL требует около четырех машинных тактов. Он работает со скоростью примерно 58 Мбит/с на 32-битном процессоре с тактовой частотой 50 МГц и является одним из самых быстрых шифров.

Примечания

1. ↑ P.Rogaway (англ.), D.Coppersmith A Software-Optimized Encryption Algorithm. — 1998.
2. ↑ U.S. Patent 5 454 039 «Software-efficient pseudorandom function and the use thereof for encryption»

Источники

• Шнайер Б. Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке Си = Applied Cryptography. Protocols, Algorithms and Source Code in C. — М.: Триумф, 2002. — С. 446—448. — 816 с. — 3000 экз. — ISBN 5-89392-055-4
• P.Rogaway (англ.), D.Coppersmith A Software-Optimized Encryption Algorithm. — 1998.
• H.Handschuh (англ.), H.Gilbert (англ.) $X^2$-Cryptanalysis of the SEAL Encryption Algorithm. — 1997.

Ссылки

• U.S. Patent 5 675 652 «Computer readable device implementing a software-efficient pseudorandom function encryption»
• Неофициальная реализация алгоритма SEAL 3.0 на языке C
• Неофициальная реализация алгоритма SEAL 3.0 на языке Delphi