- Trivium (шифр)
-
Trivium — симметричный алгоритм синхронного потокового шифрования, ориентированный, в первую очередь, на аппаратную реализацию с гибким равновесием между скоростью работы и количеством элементов, имеющий также возможность достаточно эффективной программной реализации.
Шифр был представлен в декабре 2008 года как часть портфолио европейского проекта eSTREAM, по профилю 2 (аппаратно ориентированные шифры). Авторами шифра являются Кристоф Де Канньер и Барт Пренел.
Данный потоковый шифр генерирует вплоть до
 бит выходного потока из 80 бит ключа и 80 бит IV (вектора инициализации). Это — самый простой шифр проекта eSTREAМ, который показывает отличные результаты по криптоустойчивости.
бит выходного потока из 80 бит ключа и 80 бит IV (вектора инициализации). Это — самый простой шифр проекта eSTREAМ, который показывает отличные результаты по криптоустойчивости.Содержание
Описание
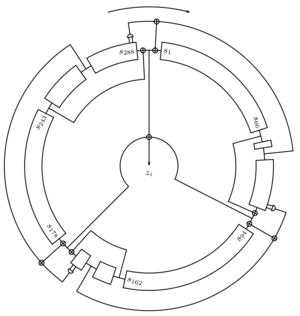
Изначальное состояние Trivium представляет собой 3 сдвиговых регистра суммарной длины в 288 бит. Каждый такт происходит изменение битов в регистрах сдвига путем нелинейной комбинации прямой и обратной связи. Для инициализации шифра ключ K и инициализирующий вектор IV записываются в 2 из 3х регистров и происходит исполнение алгоритма в течение 4х288 = 1152 раз, что гарантирует зависимость каждого бита начального состояния от каждого бита ключа и каждого бита инициализирующего вектора.
После прохождения стадии инициализации каждый такт генерируется новый член ключевого потока Z, который проходит процедуру XOR с следующим членом текста. Процедура расшифровки происходит в обратном порядке — каждый член шифротекста проходит процедуру XOR с каждым членом ключевого потока Z. [1]
Алгоритм
Потоковые шифры
Trivium генерирует последовательность Z, так называемый ключевой поток, длинной вплоть до
 бит. Для шифровки сообщения необходимо провести операцию XOR от сообщения и ключевого потока. Расшифровка производится аналогичным образом, выполняется операция XOR от шифротекста и ключевого потока.
бит. Для шифровки сообщения необходимо провести операцию XOR от сообщения и ключевого потока. Расшифровка производится аналогичным образом, выполняется операция XOR от шифротекста и ключевого потока.Инициализация
Алгоритм инициализируется загрузкой 80битного ключа и 80битного инициализирующего вектора в 288битное начальное состояние. Инициализация может быть описана следующим псевдокодом.
Процедура инициализации гарантирует то, что каждый бит начального состояния зависит от каждого бита ключа и каждого бита инициализирующего вектора. Данный эффект достигается уже после 2х полных проходов (2*288 выполнений цикла). Еще 2 прохода предназначены для усложнения битовых взаимосвязей. Для примера первые 128 байт ключевого потока Z, полученного от нулевых ключа и инициализирующего вектора, имеют примерно одинаковое количество равномерно распределенных 1 и 0. Даже при простейших и одинаковых ключах алгоритм Trivium выдает последовательность чисел, близкую к случайной.
Первые 128 байт ключевого потока, сгенерированные от нулевых K и IV в 16тиричной системе счисления0000000 e0 fb 26 bf 59 58 1b 05 7a 51 4e 2e 9f 23 7f c9 0000010 32 56 16 03 07 19 2d cf a8 e7 0f 79 b2 a1 cd e9 0000020 52 f7 03 92 68 02 38 b7 4c 2b 75 1a a2 9a 9a 59 0000030 55 28 98 49 74 6e 59 80 80 03 4c 1a a5 b5 f2 d4 0000040 34 69 bb 86 ca 52 15 b3 ae 80 12 69 73 55 9a 31 0000050 b2 6c 0e f5 16 40 20 d6 30 7f 4e 3f 48 16 dc 24 0000060 25 5c ad c4 10 a1 c9 1b bb e8 01 4e dc fc 2e 27 0000070 9e fa ae 02 a2 48 05 b2 2e fb f4 4f 27 76 56 27 0000080 3e 5e b7 06 4e e6 4a 57 7b ad a2 3a 1c 52 ff 48 0000090 f3 92 f8 87 ff 98 aa 87 e6 bf f6 19 38 3c ff 19 00000a0 3f 0a a5 fd 01 ec d0 d8 fa f0 fa 87 09 a1 4e ee 00000b0 63 29 9f 9b 31 ef 95 a5 c7 76 19 8d c7 e0 df 55 00000c0 1b 0f 50 e9 b8 91 85 ea 06 7b d5 2a ad 2b 77 f4 00000d0 ac 84 9b 6d 3f 2e a9 85 99 d7 04 95 02 33 fd f0 00000e0 b7 f8 5b 6e b7 c8 f0 b4 46 aa 20 cd a0 dd dd 4f
Как можно заметить, после 4х циклов инициализации единицы, записанные в ячейки
 ,
,  и
и  повлияли на все остальные биты начального состояния, и, таким образом, даже при простейших и одинаковых ключах каждый байт сообщения будет изменен в результате работы алгоритма шифрования.
повлияли на все остальные биты начального состояния, и, таким образом, даже при простейших и одинаковых ключах каждый байт сообщения будет изменен в результате работы алгоритма шифрования.Работа алгоритма
Генератор потока использует 15 бит из 288битного начального состояния для изменения 3х бит состояния и вычисления 1 бита ключевого потока
 . В результате работы алгоритма может быть получено до
. В результате работы алгоритма может быть получено до  бит ключевого потока. Алгоритм может быть описан следующим псевдокодом.
бит ключевого потока. Алгоритм может быть описан следующим псевдокодом.В данном псевдокоде все вычисления производятся по модулю 2. То есть операции сложения и умножения являются операциями XOR и AND.
Период
Период ключевого потока сложно определить, из-за нелинейного характера изменений начального состояния. Даже если открыть все триггеры AND, что приведет к полностью линейной схеме, можно показать, что любая пара ключа и инициализирующего вектора приведет к генерации ключевого потока с периодом порядка
 (что уже превосходит требуемую длину ключевого потока
(что уже превосходит требуемую длину ключевого потока  ).
).Если же предположить, что Trivium начинает генерировать случайный ключевой поток, после небольшого количества итераций, то все сгенерированные последовательности, длинной до
 будут равновероятны. А также вероятность того, что пара ключ/инициализирующий вектор сгенерируют ключевой поток с периодом меньше, чем
будут равновероятны. А также вероятность того, что пара ключ/инициализирующий вектор сгенерируют ключевой поток с периодом меньше, чем  будет порядка
будет порядка  .[2]
.[2]Производительность
Стандартная аппаратная реализация алгоритма требует наличия 3488 логических элементов и производит 1 бит ключевого потока за 1 такт. Но, так как каждое новое состояние бита не изменяется по крайней мере в течение 64 раундов, то еще 64 состояния могут быть сгенерированы параллельно при увеличении количества логических элементов до 5504. Также возможны различные вариации производительности в зависимости от количества использованных элементов.
Программная интерпретация данного алгоритма также достаточно эффективна. Реализация Trivium на языке C на процессоре AthlonXP 1600+ позволяет получить скорость шифрования более 2,4Мбит/с
Защищенность
В отличие от ранних потоковых шифров, как например RC4, алгоритм Trivium, кроме закрытого ключа (K) также имеет инициализирующий вектор (IV), который является открытым ключом. Применение IV позволяет проводить множество независимых сеансов шифровки/расшифровки используя всего лишь 1 ключ и несколько инициализирующих векторов (по одному для каждого сеанса). Также можно использовать несколько инициализирующих векторов для одного сеанса, используя для каждого нового сообщения новый IV
В данный момент не известно никаких методов атаки на данный алгоритм, которые были бы эффективнее последовательного перебора (или брутфорса (англ. brute force)). Сложность проведения данной атаки зависит от длины сообщения и составляет порядка
 .
.Существуют исследования методов атак (например кубическая атака[3]), которые близки по эффективности к перебору. Кроме того, существует метод атаки, позволяющий восстановить K из IV и ключевого потока. Сложность данной атаки равна
 и незначительно уменьшается при увеличении количества инициализирующих векторов, использовавшихся с одним ключом. Возможны также атаки с исследованием псевдослучайной последовательности ключевого потока с целью нахождения закономерностей и предсказания последующих бит потока, но данные атаки требуют решения сложных нелинейных уравнений. Наименьшая полученная сложность такой атаки составляет
и незначительно уменьшается при увеличении количества инициализирующих векторов, использовавшихся с одним ключом. Возможны также атаки с исследованием псевдослучайной последовательности ключевого потока с целью нахождения закономерностей и предсказания последующих бит потока, но данные атаки требуют решения сложных нелинейных уравнений. Наименьшая полученная сложность такой атаки составляет  [4][5]
[4][5]Методы исследования
Практически все достижения в области взлома Trivium представляют собой попытки применить атаки, удачно проведенные на усеченных версиях алгоритма.[1] Зачастую, в качестве исследуемого используется версия алгоритма Bivium, в котором используется всего 2 сдвиговых регистра суммарной длины 192 бита.[1]
Ссылки
- Trivium на странице проекта eSTREAM
- Описание алгоритма на странице проекта eSTREAM
- Принципы построения потоковых шифров
Примечания
Симметричные криптосистемы Поточный шифр Сеть Фейстеля ГОСТ 28147-89 • Blowfish • Camellia • CAST-128 • CAST-256 • CIPHERUNICORN-A • CIPHERUNICORN-E • CLEFIA • Cobra • DFC • DEAL • DES • DESX • EnRUPT • FEAL • FNAm2 • HPC • IDEA • KASUMI • Khufu • LOKI97 • MARS • NewDES • Raiden • RC5 • RC6 • RTEA • SEED • Sinople • TEA • Triple DES • Twofish • XTEA • XXTEA
SP-сеть Другие Категория:- Потоковые шифры
Wikimedia Foundation. 2010.