- Camellia (алгоритм)
-
Camellia Создатель: Mitsubishi, NTT
Создан: Опубликован: Размер ключа: 128, 192 или 256 бит
Размер блока: 128 бит
Число раундов: 18 или 24
Тип: Camellia — алгоритм симметричного блочного шифрования (размер блока 128 бит, ключ 128, 192, 256 бит), один из финалистов европейского конкурса NESSIE (наряду с AES и Shacal-2), разработка японских компаний Nippon Telegraph and Telephone Corporation и Mitsubishi Electric Corporation (представлен 10 марта 2000 г.). Сертифицирован японской организацией CRYPTREC как рекомендованный для промышленного и государственного использования алгоритм.
Camellia является дальнейшим развитием алгоритма шифрования E2, одного из алгоритмов, представленных на конкурсе AES и с использованием элементов алгоритма MISTY1.
Структура алгоритма основана на классической цепи Фейстеля с предварительным и финальным забеливанием. Цикловая функция использует нелинейное преобразование (S-блоки), блок линейного рассеивания каждые 16 циклов (побайтовая операция XOR) и байтовую перестановку.
В зависимости от длины ключа имеет 18 циклов (128 разрядный ключ), либо 24 цикла (192 и 256 разрядный ключ).
Поддержка алгоритма Camellia введена в 2008 году в браузере Mozilla Firefox 3. Алгоритм патентован, однако распространяется под рядом свободных лицензий, в частности, является частью проекта OpenSSL.
Содержание
Описание
Генерация вспомогательных ключей
Обозначение Значение & Побитовое И (AND) | Побитовое ИЛИ (OR) ^ Побитовое исключающее ИЛИ (XOR) << Логический сдвиг влево >> Логический сдвиг вправо <<< Циклический сдвиг влево ~y Инверсия Константа Значение MASK8 0xff MASK32 0xffffffff MASK64 0xffffffffffffffff MASK128 0xffffffffffffffffffffffffffffffff C1 0xA09E667F3BCC908B C2 0xB67AE8584CAA73B2 C3 0xC6EF372FE94F82BE C4 0x54FF53A5F1D36F1C C5 0x10E527FADE682D1D C6 0xB05688C2B3E6C1FD - 1. Ключ (К) разбивается на 2 128-битные части KL и KR.
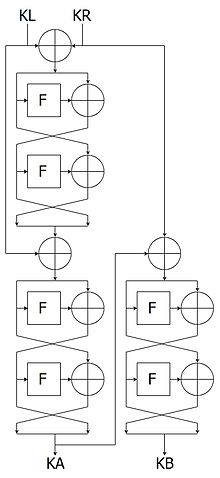
Ключ KL KR 128 K 0 192 K >> 64 ((K & MASK64) << 64) | (~(K & MASK64)) 256 K >> 128 K & MASK128 - 2. Вычисляем 128-битные числа KA и KB (см. схему). Переменные D1 и D2 64-битные.
D1 = (KL ^ KR) >> 64; D2 = (KL ^ KR) & MASK64; D2 = D2 ^ F(D1, C1); D1 = D1 ^ F(D2, C2); D1 = D1 ^ (KL >> 64); D2 = D2 ^ (KL & MASK64); D2 = D2 ^ F(D1, C3); D1 = D1 ^ F(D2, C4); KA = (D1 << 64) | D2; D1 = (KA ^ KR) >> 64; D2 = (KA ^ KR) & MASK64; D2 = D2 ^ F(D1, C5); D1 = D1 ^ F(D2, C6); KB = (D1 << 64) | D2;
- 3. Вычисляем вспомогательные 64-битные ключи kw1, ..., kw4, k1, ..., k24, ke1, ..., ke6 в зависимости от размера ключа:
128 битkw1 = (KL <<< 0) >> 64; kw2 = (KL <<< 0) & MASK64; k1 = (KA <<< 0) >> 64; k2 = (KA <<< 0) & MASK64; k3 = (KL <<< 15) >> 64; k4 = (KL <<< 15) & MASK64; k5 = (KA <<< 15) >> 64; k6 = (KA <<< 15) & MASK64; ke1 = (KA <<< 30) >> 64; ke2 = (KA <<< 30) & MASK64; k7 = (KL <<< 45) >> 64; k8 = (KL <<< 45) & MASK64; k9 = (KA <<< 45) >> 64; k10 = (KL <<< 60) & MASK64; k11 = (KA <<< 60) >> 64; k12 = (KA <<< 60) & MASK64; ke3 = (KL <<< 77) >> 64; ke4 = (KL <<< 77) & MASK64; k13 = (KL <<< 94) >> 64; k14 = (KL <<< 94) & MASK64; k15 = (KA <<< 94) >> 64; k16 = (KA <<< 94) & MASK64; k17 = (KL <<< 111) >> 64; k18 = (KL <<< 111) & MASK64; kw3 = (KA <<< 111) >> 64; kw4 = (KA <<< 111) & MASK64;
192 и 256 битkw1 = (KL <<< 0) >> 64; kw2 = (KL <<< 0) & MASK64; k1 = (KB <<< 0) >> 64; k2 = (KB <<< 0) & MASK64; k3 = (KR <<< 15) >> 64; k4 = (KR <<< 15) & MASK64; k5 = (KA <<< 15) >> 64; k6 = (KA <<< 15) & MASK64; ke1 = (KR <<< 30) >> 64; ke2 = (KR <<< 30) & MASK64; k7 = (KB <<< 30) >> 64; k8 = (KB <<< 30) & MASK64; k9 = (KL <<< 45) >> 64; k10 = (KL <<< 45) & MASK64; k11 = (KA <<< 45) >> 64; k12 = (KA <<< 45) & MASK64; ke3 = (KL <<< 60) >> 64; ke4 = (KL <<< 60) & MASK64; k13 = (KR <<< 60) >> 64; k14 = (KR <<< 60) & MASK64; k15 = (KB <<< 60) >> 64; k16 = (KB <<< 60) & MASK64; k17 = (KL <<< 77) >> 64; k18 = (KL <<< 77) & MASK64; ke5 = (KA <<< 77) >> 64; ke6 = (KA <<< 77) & MASK64; k19 = (KR <<< 94) >> 64; k20 = (KR <<< 94) & MASK64; k21 = (KA <<< 94) >> 64; k22 = (KA <<< 94) & MASK64; k23 = (KL <<< 111) >> 64; k24 = (KL <<< 111) & MASK64; kw3 = (KB <<< 111) >> 64; kw4 = (KB <<< 111) & MASK64;
Шифрование
Шифрование происходит по схеме Фейстеля с 18 этапами для 128-битного ключа и 24 этапами для 192- и 256-битных ключей. Каждые 6 этапов применяются функции FL и FLINV.
128 битD1 = M >> 64; // Шифруемое сообщение делится на две 64-битные части D2 = M & MASK64; D1 = D1 ^ kw1; // Предварительное забеливание D2 = D2 ^ kw2; D2 = D2 ^ F(D1, k1); D1 = D1 ^ F(D2, k2); D2 = D2 ^ F(D1, k3); D1 = D1 ^ F(D2, k4); D2 = D2 ^ F(D1, k5); D1 = D1 ^ F(D2, k6); D1 = FL (D1, ke1); // FL D2 = FLINV(D2, ke2); // FLINV D2 = D2 ^ F(D1, k7); D1 = D1 ^ F(D2, k8); D2 = D2 ^ F(D1, k9); D1 = D1 ^ F(D2, k10); D2 = D2 ^ F(D1, k11); D1 = D1 ^ F(D2, k12); D1 = FL (D1, ke3); // FL D2 = FLINV(D2, ke4); // FLINV D2 = D2 ^ F(D1, k13); D1 = D1 ^ F(D2, k14); D2 = D2 ^ F(D1, k15); D1 = D1 ^ F(D2, k16); D2 = D2 ^ F(D1, k17); D1 = D1 ^ F(D2, k18); D2 = D2 ^ kw3; // Финальное забеливание D1 = D1 ^ kw4; C = (D2 << 64) | D1;
192 и 256 битD1 = M >> 64; // Шифруемое сообщение делится на две 64-битные части D2 = M & MASK64; D1 = D1 ^ kw1; // Предварительное забеливание D2 = D2 ^ kw2; D2 = D2 ^ F(D1, k1); D1 = D1 ^ F(D2, k2); D2 = D2 ^ F(D1, k3); D1 = D1 ^ F(D2, k4); D2 = D2 ^ F(D1, k5); D1 = D1 ^ F(D2, k6); D1 = FL (D1, ke1); // FL D2 = FLINV(D2, ke2); // FLINV D2 = D2 ^ F(D1, k7); D1 = D1 ^ F(D2, k8); D2 = D2 ^ F(D1, k9); D1 = D1 ^ F(D2, k10); D2 = D2 ^ F(D1, k11); D1 = D1 ^ F(D2, k12); D1 = FL (D1, ke3); // FL D2 = FLINV(D2, ke4); // FLINV D2 = D2 ^ F(D1, k13); D1 = D1 ^ F(D2, k14); D2 = D2 ^ F(D1, k15); D1 = D1 ^ F(D2, k16); D2 = D2 ^ F(D1, k17); D1 = D1 ^ F(D2, k18); D1 = FL (D1, ke5); // FL D2 = FLINV(D2, ke6); // FLINV D2 = D2 ^ F(D1, k19); D1 = D1 ^ F(D2, k20); D2 = D2 ^ F(D1, k21); D1 = D1 ^ F(D2, k22); D2 = D2 ^ F(D1, k23); D1 = D1 ^ F(D2, k24); D2 = D2 ^ kw3; // Финальное забеливание D1 = D1 ^ kw4; C = (D2 << 64) | D1;
Вспомогательные функции F, FL, FLINV
F-, FL- и FLINV-функции на вход получают 2 64-битных параметра - данные F_IN и ключ KE.
Функция F использует 16 8-битных переменных t1, ..., t8, y1, ..., y8 и 1 64-битную переменную. На выходе функции 64-битное число.
Функции FL и FLINV используют 4 32-битные переменные x1,x2,k1,k2. На выходе функции 64-битное число. Функция FLINV - обратная к FLF-функцияx = F_IN ^ KE; t1 = x >> 56; t2 = (x >> 48) & MASK8; t3 = (x >> 40) & MASK8; t4 = (x >> 32) & MASK8; t5 = (x >> 24) & MASK8; t6 = (x >> 16) & MASK8; t7 = (x >> 8) & MASK8; t8 = x & MASK8; t1 = SBOX1[t1]; t2 = SBOX2[t2]; t3 = SBOX3[t3]; t4 = SBOX4[t4]; t5 = SBOX2[t5]; t6 = SBOX3[t6]; t7 = SBOX4[t7]; t8 = SBOX1[t8]; y1 = t1 ^ t3 ^ t4 ^ t6 ^ t7 ^ t8; y2 = t1 ^ t2 ^ t4 ^ t5 ^ t7 ^ t8; y3 = t1 ^ t2 ^ t3 ^ t5 ^ t6 ^ t8; y4 = t2 ^ t3 ^ t4 ^ t5 ^ t6 ^ t7; y5 = t1 ^ t2 ^ t6 ^ t7 ^ t8; y6 = t2 ^ t3 ^ t5 ^ t7 ^ t8; y7 = t3 ^ t4 ^ t5 ^ t6 ^ t8; y8 = t1 ^ t4 ^ t5 ^ t6 ^ t7; F_OUT = (y1 << 56) | (y2 << 48) | (y3 << 40) | (y4 << 32)| (y5 << 24) | (y6 << 16) | (y7 << 8) | y8;FL-функцияvar x1, x2 as 32-bit unsigned integer; var k1, k2 as 32-bit unsigned integer; x1 = FL_IN >> 32; x2 = FL_IN & MASK32; k1 = KE >> 32; k2 = KE & MASK32; x2 = x2 ^ ((x1 & k1) <<< 1); x1 = x1 ^ (x2 | k2); FL_OUT = (x1 << 32) | x2;FLINV-функцияvar y1, y2 as 32-bit unsigned integer; var k1, k2 as 32-bit unsigned integer; y1 = FLINV_IN >> 32; y2 = FLINV_IN & MASK32; k1 = KE >> 32; k2 = KE & MASK32; y1 = y1 ^ (y2 | k2); y2 = y2 ^ ((y1 & k1) <<< 1); FLINV_OUT = (y1 << 32) | y2;S - блоки
Значение функции SBOX1 определяется из следующей таблицы:
0 1 2 3 4 5 6 7 8 9 a b c d e f 0 112 130 44 236 179 39 192 229 228 133 87 53 234 12 174 65 1 35 239 107 147 69 25 165 33 237 14 79 78 29 101 146 189 2 134 184 175 143 124 235 31 206 62 48 220 95 94 197 11 26 3 166 225 57 202 213 71 93 61 217 1 90 214 81 86 108 77 4 139 13 154 102 251 204 176 45 116 18 43 32 240 177 132 153 5 223 76 203 194 52 126 118 5 109 183 169 49 209 23 4 215 6 20 88 58 97 222 27 17 28 50 15 156 22 83 24 242 34 7 254 68 207 178 195 181 122 145 36 8 232 168 96 252 105 80 8 170 208 160 125 161 137 98 151 84 91 30 149 224 255 100 210 9 16 196 0 72 163 247 117 219 138 3 230 218 9 63 221 148 a 135 92 131 2 205 74 144 51 115 103 246 243 157 127 191 226 b 82 155 216 38 200 55 198 59 129 150 111 75 19 190 99 46 c 233 121 167 140 159 110 188 142 41 245 249 182 47 253 180 89 d 120 152 6 106 231 70 113 186 212 37 171 66 136 162 141 250 e 114 7 185 85 248 238 172 10 54 73 42 104 60 56 241 164 f 64 40 211 123 187 201 67 193 21 227 173 244 119 199 128 158 Для примера: SBOX1(0x7a)=232.
SBOX2, SBOX3 и SBOX4 определяются из SBOX1 следующим образом:SBOX2[x] = SBOX1[x] <<< 1; SBOX3[x] = SBOX1[x] <<< 7; SBOX4[x] = SBOX1[x <<< 1];Расшифрование
Алгоритм расшифрования идентичен шифрованию, с тем лишь различием, что вспомогательные ключи меняются местами по следующей схеме, в зависимости от длины исходного ключа:
Размер ключа 128 бит 192 или 256 бит kw1 <-> kw3 kw1 <-> kw3 kw2 <-> kw4 kw2 <-> kw4 k1 <-> k18 k1 <-> k24 k2 <-> k17 k2 <-> k23 k3 <-> k16 k3 <-> k22 k4 <-> k15 k4 <-> k21 k5 <-> k14 k5 <-> k20 k6 <-> k13 k6 <-> k19 k7 <-> k12 k7 <-> k18 k8 <-> k11 k8 <-> k17 k9 <-> k10 k9 <-> k16 k10 <-> k15 k11 <-> k14 k12 <-> k13 ke1 <-> ke4 ke1 <-> ke6 ke2 <-> ke3 ke2 <-> ke5 ke3 <-> ke4 Пример шифрования
Ключ: 0123456789abcdeffedcba9876543210
Шифруемое сообщение: 0123456789abcdeffedcba9876543210
Зашифрованное сообщение: 67673138549669730857065648eabe43
Ключиk[1]=ae71c3d55ba6bf1d k[2]=169240a795f89256 k[3]=a2b3c4d5e6f7ff6e k[4]=5d4c3b2a19080091 k[5]=e1eaadd35f8e8b49 k[6]=2053cafc492b5738 k[7]=79bdffdb97530eca k[8]=8642002468acf135 k[9]=d7e3a2d24814f2bf k[10]=00123456789abcde k[11]=d169240a795f8925 k[12]=6ae71c3d55ba6bf1 k[13]=1d950c840048d159 k[14]=e26af37bffb72ea6 k[15]=e57e2495ab9c70f5 k[16]=56e9afc745a49029 kw[1]=0123456789abcdef kw[2]=fedcba9876543210 kw[3]=492b5738e1eaadd3 kw[4]=5f8e8b492053cafc ke[1]=56e9afc745a49029 ke[2]=e57e2495ab9c70f5 ke[3]=97530eca86420024 ke[4]=68acf13579bdffdb
Криптостойкость
По словам авторов алгоритма:
Мы доказали, что успех дифференциального[1] и линейного [2] криптоанализов практически невозможнен против полного цикла Camellia с 18 этапами. Более того, Camellia был разработан для того, чтобы противостоять более сложным криптографическим атакам, таким как дифференциальные атаки высоких порядков[3][4], интерполяционные атаки[5][6], атаки "на связанных ключах"[7][8], укороченные дифференциальные атаки[9][10] и другие
Оригинальный текст (англ.)We confirmed that it is extremely unlikely that differential and linear attacks will succeed against the full 18-round Camellia. Moreover, Camellia was designed to offer security against other advanced cryptanalytic attacks including higher order differential attacks, interpolation attacks, related-key attacks, truncated differential attacks, and so on
Применение
Поддержка Camellia была добавлена в финальной версии Mozilla Firefox 3 в 2008 году[11]. Позднее в том же году команда разработчиков FreeBSD объявила, что поддержка данного шифрования также была включена в FreeBSD 6.4-RELEASE. В сентябре 2009 года GNU Privacy Guard добавили поддержку Camellia в версии 1.4.10. Кроме того, многие популярные библиотеки безопасности, такие как Crypto++, GnuTLS, PolarSSL и OpenSSL[12] также включают в себя поддержку Camellia.
Сравнение с аналогами
Алгоритм Количество логических элементов Время вычисления ключей, нс Время шифрования/дешифрования, нс Пропускная способность, Mb/s Шифрование/дешифрование Ключи Полное количество DES 42,204 12,201 54,405 - 55.11 1161.31 Triple-DES 124,888 23,207 128,147 - 157.09 407.40 MARS 690,654 2,245,096 2,935,754 1740.99 567.49 225.55 RC6 741,641 901,382 1,643,037 2112.26 627.57 203.96 Rijndael 518,508 93,708 612,834 57.39 65.64 1950.03 Serpent 298,533 205,096 503,770 114.07 137.40 931.58 Twofish 200,165 231,682 431,857 16.38 324.80 394.08 Camellia 216,911 55,907 272,819 24.36 109.35 1170.55 Разработчики
- Kazumaro Aoki
- Tetsuya Ichikawa
- Masayuki Kanda
- Mitsuru Matsui
- Shiho Moriai
- Junko Nakajima
- Toshio Tokita
- Nippon Telegraph and Telephone Corporation
- Mitsubishi Electric Corporation
См. также
Примечания
- ↑ M. Matsui,Linear Cryptanalysis Method for DES Cipher - Lecture Notes in Computer Science, стр.386–397, Springer-Verlag, 1994
- ↑ E. Biham and A. Shamir, Linear Cryptanalysis Method for DES Cipher - Differential Cryptanalysis of the Data Encryption Standard, Springer-Verlag, 1994
- ↑ L.R.Knudsen, “Truncated and Higher Order Differentials,” Fast Software Encryption — Second In-ternational Workshop, Lecture Notes in ComputerScience 1008, pp.196–211, Springer-Verlag, 1995.
- ↑ T. Jakobsen and L. R. Knudsen, The Interpolation Attack on Block Ciphers, Fast Software Encryption, FSE’97, Lecture Notes in Computer Sci-ence 1267, pp.28–40, Springer-Verlag, 1997.
- ↑ T. Jakobsen and L. R. Knudsen, The Interpolation Attack on Block Ciphers, Fast Software Encryption, FSE’97, Lecture Notes in Computer Science 1267, pp.28–40, Springer-Verlag, 1997.
- ↑ K. Aoki, “Practical Evaluation of Security against Generalized Interpolation Attack,” IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences (Japan), Vol.E83-A, No.1, pp.33–38, 2000.
- ↑ E. Biham, New Types of Cryptanalytic Attacks Using Related Keys, Journal of Cryptology, Vol.7, No.4, pp.229–246, Springer-Verlag, 1994.
- ↑ J.Kelsey, B.Schneier and D.Wagner, “Key-Schedule Cryptanalysis of IDEA, G-DES, GOST, SAFER, and Triple-DES,” Advances in Cryptology — CRYPTO’96, Lecture Notes in Computer Science 1109, pp.237–251, Springer-Verlag, 1996.
- ↑ L.R.Knudsen, Truncated and Higher Order Dif-ferentials, Fast Software Encryption — Second International Workshop, Lecture Notes in Computer Science 1008, pp.196–211, Springer-Verlag, 1995.
- ↑ M. Matsui and T. Tokita, Cryptanalysis of a Reduced Version of the Block Cipher E2, Fast Software Encryption — 6th International Workshop, FSE’99, Lecture Notes in Computer Science 1636, pp.71–80, Springer-Verlag, 1999.
- ↑ Camellia cipher added to Firefox. Mozilla in Asia. Mozilla (July 30, 2009). Архивировано из первоисточника 29 февраля 2012.
- ↑ NTT (2006-11-08). The Open Source Community OpenSSL Project Adopts the Next Generation International Standard Cipher "Camellia" Developed in Japan. Пресс-релиз. Проверено 2008-02-29.
- ↑ Kazumaro Aoki, Tetsuya Ichikawa, Masayuki Kanda, Mitsuru Matsui, Shiho Moriai, Junko Nakajima and Toshio Tokita Camellia : A 128-Bit Block Cipher Suitable for Multiple Platforms — Design and Analysis
Ссылки
- Официальная страница Camellia (англ.)
- RFC 3713 Описание алгоритма Camellia (англ.)
- RFC 3657 Использование алгоритма Camellia в CMS
- RFC 4312 Использование алгоритма Camellia в IPsec
- Пример программной реализации (англ.)
- Сравнение скорости шифрования различных алгоритмов (англ.)
Симметричные криптосистемы Поточный шифр Сеть Фейстеля ГОСТ 28147-89 • Blowfish • Camellia • CAST-128 • CAST-256 • CIPHERUNICORN-A • CIPHERUNICORN-E • CLEFIA • Cobra • DFC • DEAL • DES • DESX • EnRUPT • FEAL • FNAm2 • HPC • IDEA • KASUMI • Khufu • LOKI97 • MARS • NewDES • Raiden • RC5 • RC6 • RTEA • SEED • Sinople • TEA • Triple DES • Twofish • XTEA • XXTEA
SP-сеть Другие Категория:- Сеть Фейстеля
Wikimedia Foundation. 2010.