Пифагоровы числа

В математике пифагоровыми числами (пифагоровой тройкой) называется кортеж из трёх целых чисел 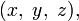$(x,\;y,\;z),$ удовлетворяющих соотношению Пифагора:

x 2 + y 2 = z 2 .

Содержание

1 Свойства
2 Примеры
3 История
4 См. также
5 Ссылки

Свойства

Поскольку уравнение $x 2 + y 2 = z 2$ однородно, при домножении $x$ , $y$ и $z$ на одно и то же число получится другая пифагорова тройка. Пифагорова тройка называется примитивной, если она не может быть получена таким способом, то есть 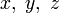$x,\;y,\;z$ — взаимно простые числа.

Треугольник, стороны которого равны пифагоровым числам, является прямоугольным. Кроме того, любой такой треугольник является героновым, то есть таким, у которого все стороны и площадь являются целочисленными. Простейший из них — египетский треугольник со сторонами 3, 4 и 5 ( $32 + 4 2 = 5 2$ ).

Пифагорова тройка 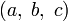$(a,\;b,\;c)$ задаёт точку с рациональными координатами 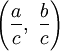$\left( \frac a c,\;\frac b c \right)$ на единичной окружности $x 2 + y 2 = 1$ .

Нетрудно видеть, что в примитивной тройке $(x, y, z)$ числа x и y имеют разную чётность. Любая примитивная пифагорова тройка $(x, y, z)$ , где x - нечётно, а y - чётно, однозначно представляется в виде 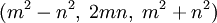$(m^2-n^2,\;2mn,\;m^2+n^2)$ для некоторых натуральных взаимно простых чисел $m > n$ разной чётности. Наоборот, любая такая пара 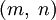$(m,\;n)$ задаёт примитивную пифагорову тройку 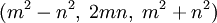$(m^2-n^2,\;2mn,\;m^2+n^2)$ . ^[1]

Примеры

Некоторые пифагоровы тройки (отсортированы по возрастанию максимального числа, выделены примитивные):

(3, 4, 5), (6, 8, 10), (5, 12, 13), (9, 12, 15), (8, 15, 17), (12, 16, 20), (15, 20, 25), (7, 24, 25), (10, 24, 26), (20, 21, 29), (18, 24, 30), (16, 30, 34), (21, 28, 35), (12, 35, 37), (15, 36, 39), (24, 32, 40), (9, 40, 41), (14, 48, 50), (30, 40, 50)…

Основываясь на свойствах чисел Фибоначчи, можно составить из них, например, такие пифагоровы тройки:

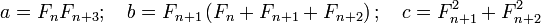$a=F_n F_{n+3};\quad b=F_{n+1}\left(F_n+F_{n+1}+F_{n+2}\right); \quad c=F_{n+1}^2+F^2_{n+2}$ .

История

Пифагоровы тройки известны очень давно. В архитектуре древнемесопотамских надгробий встречается равнобедренный треугольник, составленный из двух прямоугольных со сторонами 9, 12 и 15 локтей. Пирамиды фараона Снофру (XXVII век до н. э.) построены с использованием треугольников со сторонами 20, 21 и 29, а также 18, 24 и 30 десятков египетских локтей.

См. также

Ссылки

↑ В. Н. Серпинский Пифагоровы треугольники. — М.: Учпедгиз, 1959. — 111 с.

Е. А. Горин Степени простых чисел в составе пифагоровых троек // Математическое просвещение. — 2008. — В. 12. — С. 105-125.

Wikimedia Foundation. 2010.

Игры ⚽ Поможем написать курсовую

Полезное

Смотреть что такое "Пифагоровы числа" в других словарях:

ПИФАГОРОВЫ ЧИСЛА — тройки таких натуральных чисел, что треугольник, длины сторон которого пропорциональны (или равны) этим числам, является прямоугольным, напр. тройка чисел: 3, 4, 5 … Большой Энциклопедический словарь
Пифагоровы числа — тройки таких натуральных чисел, что треугольник, длины сторон которого пропорциональны (или равны) этим числам, является прямоугольным, например тройка чисел: 3, 4, 5. * * * ПИФАГОРОВЫ ЧИСЛА ПИФАГОРОВЫ ЧИСЛА, тройки таких натуральных чисел, что… … Энциклопедический словарь
Пифагоровы числа — тройки натуральных чисел таких, что треугольник, длины сторон которого пропорциональны (или равны) этим числам, является прямоугольным. По теореме, обратной теореме Пифагора (см. Пифагора теорема), для этого достаточно, чтобы они… … Большая советская энциклопедия
ПИФАГОРОВЫ ЧИСЛА — тройки целых положительных чисел х, у,z, удовлетворяющих уравнению x2+у 2=z2. Все решения этого уравнения, а следовательно, и все П. ч. выражаются формулами х=а 2 b2, y=2ab, z=a2+b2, где а, b произвольные целые положительные числа ( а>b). П. ч … Математическая энциклопедия
ПИФАГОРОВЫ ЧИСЛА — тройки таких натуральных чисел, что треугольник, длины сторон к рого пропорциональны (или равны) этим числам, является прямоугольным, напр. тройка чисел: 3, 4, 5 … Естествознание. Энциклопедический словарь
Пифагоровы тройки — В математике пифагоровыми числами (пифагоровой тройкой) называется кортеж из трёх целых чисел удовлетворяющих соотношению Пифагора: x2 + y2 = z2. Содержание 1 Свойства 2 Примеры … Википедия
Фигурные числа — Фигурные числа общее название чисел, связанных с той или иной геометрической фигурой. Это историческое понятие восходит к пифагорейцам. Предположительно от фигурных чисел возникло выражение: «Возвести число в квадрат или в куб». Содержание… … Википедия
Многоугольные числа — Фигурные числа общее название чисел, связанных с той или иной геометрической фигурой. Это историческое понятие восходит к пифагорейцам. Различают следующие виды фигурных чисел: Линейные числа числа, не разлагающиеся на сомножители, то есть их… … Википедия
Парадокс числа Пи — «Парадокс числа пи» шутка на тему математики, имевшая хождение в среде студентов до 80 х годов (фактически, до массового распространения микрокалькуляторов) и была связана с ограниченной точностью вычислений тригонометрических функций и… … Википедия
Арифметика — (греч. arithmetika, от arithmys число) наука о числах, в первую очередь о натуральных (целых положительных) числах и (рациональных) дробях, и действиях над ними. Владение достаточно развитым понятием натурального числа и умение… … Большая советская энциклопедия

Словари и энциклопедии на Академике

Пифагоровы числа