Формулы Френеля

Переменные, используемые в уравнениях Френеля

Частичное пропускание и отражение амплитуды волны, бегущей в среде от низкого к высокому преломляющему индексу

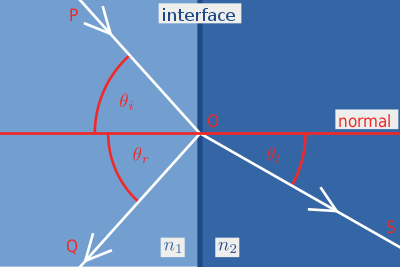
Фо́рмулы Френе́ля определяют амплитуды и интенсивности преломлённой и отражённой электромагнитной волны при прохождении через плоскую границу раздела двух сред с разными показателями преломления. Названы в честь Огюста Френеля, французского физика, который их вывел. Отражение света, описываемое формулами Френеля, называется френелевским отражением.

Формулы Френеля справедливы в том случае, когда граница раздела двух сред гладкая, среды изотропны, угол отражения равняется углу падения, а угол преломления определяется законом Снеллиуса. В случае неровной поверхности, особенно когда характерные размеры неровностей одного порядка с длиной волны, большое значение имеет диффузное рассеяние света на поверхности.

При падении на плоскую границу различают две поляризации света. s-Поляризация — это поляризация света, для которой напряжённость электрического поля электромагнитной волны перпендикулярна плоскости падения (т.е. плоскости, в которой лежат и падающий, и отражённый луч). p-Поляризация — поляризация света, для которой вектор напряжённости электрического поля лежит в плоскости падения.

Формулы Френеля для s-поляризации и p-поляризации различаются. Поскольку свет с разными поляризациями по-разному отражается от поверхности, то отражённый свет всегда частично поляризован, даже если падающий свет неполяризован. Угол падения, при котором отражённый луч полностью поляризован, называется углом Брюстера; он зависит от отношения показателей преломления сред, образующих границу раздела.

s-Поляризация

s-Поляризация — это поляризация света, для которой напряжённость электрического поля электромагнитной волны перпендикулярна плоскости падения (т.е. плоскости, в которой лежат и падающий, и отражённый луч).

$S = \frac{2}{1+\frac{\mu_1\mathrm{tg\,}\theta_i}{\mu_2\mathrm{tg\,}\theta_t}}P\rightarrow \frac{2\cos\theta_i\sin\theta_t}{\sin(\theta_i+\theta_t)}P, \qquad Q = \frac{1-\frac{\mu_1\mathrm{tg\,}\theta_i}{\mu_2\mathrm{tg\,}\theta_t}}{1+\frac{\mu_1\mathrm{tg\,}\theta_i}{\mu_2\mathrm{tg\,}\theta_t}}P\rightarrow -\frac{\sin(\theta_i-\theta_t)}{\sin(\theta_i+\theta_t)}P,$

где $\theta_i$ — угол падения, $\theta_t$ — угол преломления, $\mu_1$ — магнитная проницаемость среды, из которой падает волна, $\mu_2$ — магнитная проницаемость среды, в которую волна проходит, $P$ — амплитуда волны, которая падает на границу раздела, $Q$ — амплитуда отражённой волны, $S$ — амплитуда преломлённой волны. В оптическом диапазоне частот $\mu=1$ с хорошей точностью и выражения упрощаются до указанных после стрелок^[1].

Углы падения и преломления для $\mu=1$ связаны между собой законом Снеллиуса

$\frac{\sin\theta_i}{\sin\theta_t} = \frac{n_2}{n_1}.$

Отношение $n = n_2/n_1$ называется относительным показателем преломления двух сред.

Коэффициент отражения

$R_s = \frac{|Q|^2}{|P|^2} = \frac{\sin^2(\theta_i -\theta_t)}{\sin^2(\theta_i + \theta_t)}.$

Коэффициент пропускания

$T_s = 1 - R_s.$

Обратите внимание, коэффициент пропускания не равен $\frac{|S|^2}{|P|^2}$, так как волны одинаковой амплитуды в разных средах несут разную энергию.

p-Поляризация

p-Поляризация — поляризация света, для которой вектор напряжённости электрического поля лежит в плоскости падения.

$S = 2\sqrt\frac{\mu_1\varepsilon_1}{\mu_2\varepsilon_2}\frac{\sin 2\theta_i}{\frac{\mu_1}{\mu_2}\sin2\theta_i+\sin 2\theta_t}P \rightarrow \frac{2\cos \theta_i\sin \theta_t}{\sin(\theta_i+\theta_t)\cos(\theta_i-\theta_t)}P,$

$Q = \frac{\frac{\mu_1}{\mu_2}\sin2\theta_i-\sin 2\theta_t}{\frac{\mu_1}{\mu_2}\sin2\theta_i+\sin 2\theta_t}P \rightarrow \frac{\mathrm{tg\,}(\theta_t-\theta_i)}{\mathrm{tg\,}(\theta_i+\theta_t)}P,$

где $P$, $Q$ и $S$ — амплитуды волны, которая падает на границу раздела, отражённой волны и преломлённой волны, соответственно, а выражения после стрелок вновь соответствуют случаю $\mu_1=\mu_2$^[1].

Коэффициент отражения

$R_p = \frac{\text{tg}^2(\theta_i -\theta_t)}{\text{tg}^2(\theta_i + \theta_t)}.$

Коэффициент пропускания

$T_p = \frac{\sin2\theta_i \sin2\theta_t}{\sin^2(\theta_i + \theta_t)\cos^2(\theta_i - \theta_t)}.$

Нормальное падение

В важном частном случае нормального падения света исчезает разница в коэффициентах отражения и пропускания для p- и s-поляризованных волн. Для нормального падения

$R_s = \left| \frac{n_2-n_1}{n_2+n_1}\right|^2,$

$T_s = \frac{4 n_1 n_2}{(n_2+n_1)^2}.$

Примечания

1. ↑ ^{1 2} Джексон Дж. Классическая электродинамика. М.: Мир, 1965

Литература

• Сивухин Д. В. Общий курс физики. — М.. — Т. IV. Оптика.
• Борн М., Вольф Э. Основы оптики. — «Наука», 1973.
• Колоколов А. А. Формулы Френеля и принцип причинности // УФН. — 1999. — Т. 169. — С. 1025.