- ФРЕНЕЛЯ ИНТЕГРАЛЫ
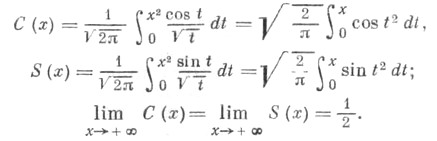
Ф. и. представляют в виде рядов
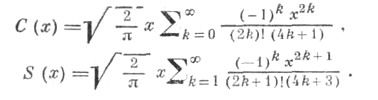
Асимптотич. представление при больших х:


В прямоугольной системе координат ( х, y )проекциями кривой

где t - действительный параметр, на координатные плоскости являются Корню спираль и кривые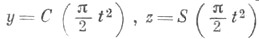 (см. рис. 2). Обобщенными Ф. и. (см. [1]) наз. функции вида:
(см. рис. 2). Обобщенными Ф. и. (см. [1]) наз. функции вида: 
Ф. и. связаны с обобщенными Ф. и. следующим образом: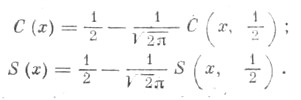
Лит.:[1] Бейтмен Г., Эрдейи А., Высшие трансцендентные функции. Функции Бесселя, функции параболического цилиндра, ортогональные многочлены, пер. с англ., 2 изд., М., 1974; [2] Янке Е., Эмде Ф., Лёш Ф., Специальные функции. Формулы, графики, таблицы, пер. с нем., 3 изд., М., 1977.
А. Б. Иванов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
